Question

11．在△ABC中，AB=AC．
（1）若D为AC的中点，BD把三角形的周长分别24cm和30cm两部分，求△ABC三边的长．
（2）若D为AC上一点，试说明AC＞$\frac{1}{2}$（BD+DC）

Answer 1

分析 （1）分两种情况讨论：当AB+AD=30，BC+DC=24或AB+AD=24，BC+DC=30，所以根据等腰三角形的两腰相等和中线的性质可求得，三边长为16，16，22或20，20，14；
（2）根据三角形两边之和大于第三边即可得到AC＞$\frac{1}{2}$（BD+DC）．

解答 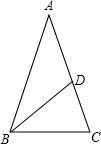解：（1）设三角形的腰AB=AC=x，
若AB+AD=24cm，
则：x+$\frac{1}{2}$x=24
∴x=16
三角形的周长为24+30=54cm
所以三边长分别为16，16，22；
若AB+AD=30cm，
则：x+$\frac{1}{2}$x=30
∴x=20
∵三角形的周长为24+30=54cm
∴三边长分别为20，20，14；
因此，三角形的三边长为16，16，22或20，20，14．

（2）∵AC=AD+CD，AB=AC，
∴2AC=AB+AD+CD＞BD+DC，
∴AC＞$\frac{1}{2}$（BD+DC）．

点评 本题主要考查了等腰三角形的性质；解题的关键是利用等腰三角形的两腰相等和中线的性质求出腰长，再利用周长的概念求得边长．同时考查了三角形三边关系．