
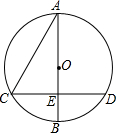
 如图,以AB为直径的⊙O与弦CD相交于点E,若AC=2$\sqrt{3}$,AE=3,CE=$\sqrt{3}$,求弧BD的长度.(保留π)
如图,以AB为直径的⊙O与弦CD相交于点E,若AC=2$\sqrt{3}$,AE=3,CE=$\sqrt{3}$,求弧BD的长度.(保留π) 分析 连接OC,先根据勾股定理的逆定理得出△ACE是直角三角形,再由垂径定理得出CE=DE,$\widehat{BC}=\widehat{BD}$,由三角函数求出∠A=30°,由圆周角定理求出∠BOC,由弧长公式得出$\widehat{BD}$的长度=$\widehat{BC}$的长度=$\frac{2}{3}$π即可.
解答 解:∵AC=2$\sqrt{3}$,AE=3,CE=$\sqrt{3}$,
∴AE2+CE2=AC2,
∴△ACE是直角三角形,∠AEC=90°,
∴CD⊥AB,sin∠A=$\frac{CE}{AC}$=$\frac{1}{2}$,
∴$\widehat{BC}=\widehat{BD}$,∠A=30°,
连接OC,如图所示:
则∠BOC=2∠A=60°,OC=$\frac{CE}{sin60°}$=$\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}$=2,
∴$\widehat{BD}$的长度=$\widehat{BC}$的长度=$\frac{60π×2}{180}$=$\frac{2}{3}$π.
点评 本题考查的是垂径定理、勾股定理的逆定理、三角函数、弧长公式等知识;熟练掌握勾股定理的逆定理,由垂径定理得出$\widehat{BC}=\widehat{BD}$是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省七年级下学期第一次月考数学试卷(解析版) 题型:单选题
下列计算正确的是( )
A. a2+a2=a4 B. 2a﹣a=2 C. (ab)2=a2b2 D. (a2)3=a5
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2017届江苏省连云港市灌云县西片九年级下学期第一次月考数学试卷(解析版) 题型:填空题
一个圆锥的侧面展开图是半径为8cm、圆心角为120°的扇形,则此圆锥底面圆的半径为__.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com