
【题目】如图 1,AB∥CD,点 E 在 AB 上,点 M 在 CD 上,点 F 在直线 AB,CD 之间,连接 EF、FM, EF⊥FM,∠CMF=140°.
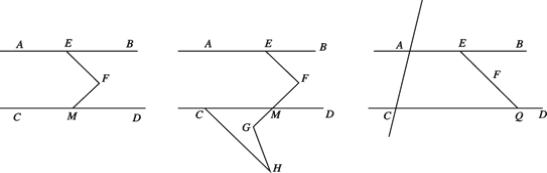
图 1 图 2 图 3
(1)直接写出∠AEF 的度数为 ________;
(2)如图 2,延长 FM 到 G,点 H 在 FG 的下方,连接 GH,CH,若∠FGH=∠H+90°, 求∠MCH 的度数;
(3)如图 3,作直线 AC,延长 EF 交 CD 于点 Q,P 为直线 AC 上一动点,探究∠PEQ,∠PQC 和∠EPQ 的数量关系,请直接给出结论.(题中所有角都是大于 0°小于 180°的角)
【答案】(1)130°;(2)50°;(3)当P点在CD的下方时,∠PEQ+∠EPQ+∠PQC=130°.当P点在CD的上方时,∠PEQ+∠EPQ+∠PQC=230°.
【解析】
(1)延长FP交AB于点Q,根据三角形的外角性质和平行线性质证明即可;
(2)延长HG交CD于点Q,根据三角形的外角性质和平行线性质证明即可;
(3)过P点作PN∥AB,根据平行线性质证明即可.
(1)延长MF交AB于点N,如图1,
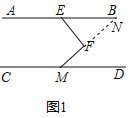
∵AB∥CD,
∴∠CMF+∠ENF=180°,
∴∠ANF=180°-140°=40°,
∵EF⊥FM,
∴∠EFN=90°,
∴∠AEF=∠ANF+∠EFN=40°+90°=130°;
故答案为:130°.
(2)延长HG交CD于点Q,如图2,
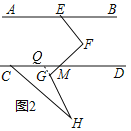
∵∠CMF=140°.
∴∠FMD=180°-140°=40°,
∴∠CMG=40°,
∵∠MQH=∠H+∠HCM,∠FGH=∠H+90°,
∴∠FGH=∠MQH+∠CMG=∠H+∠HCM+∠CMG,
∴∠HCM+∠CMG=90°,
∴∠MCH=90°-40°=50°;
(3)过P点作PN∥AB,如图3,
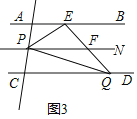
由(1)可知,∠AEF=130°,
∴∠AEP+∠PEQ=130°,
∵AB∥CD,
∴AB∥PN∥CD,
∴∠AEP=∠EPN,∠NPQ=∠PQC,
∴∠EPN=∠EPQ-∠NPQ=∠EPQ-∠PQC,
∴∠PEQ+∠EPQ-∠PQC=130°.
当P点在CD的下方时,∠PEQ+∠EPQ+∠PQC=130°.
当P点在CD的上方时,∠PEQ+∠EPQ+∠PQC=230°.


科目:初中数学 来源: 题型:
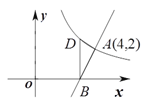
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() 的值及点
的值及点![]() 的坐标;
的坐标;
(2)过点![]() 作
作![]()
![]() 轴交反比例函数的图象于点
轴交反比例函数的图象于点![]() ,求点D的坐标和
,求点D的坐标和![]() 的面积;
的面积;
(3)观察图象,写出当x>0时不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】供电局的电力维修工要到30千米远的郊区进行电力抢修.技术工人骑摩托车先走,15分钟后,抢修车装载着所需材料出发,结果他们同时到达.已知抢修车的速度是摩托车的1.5倍,求这两种车的速度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中有3个分别标有数字-1、1、2的小球,它们除标的数字不同外无其他区别.
(1)随机地从口袋中取出一小球,求取出的小球上标的数字为负数的概率;
(2)随机地从口袋中取出一小球,放回后再取出第二个小球,求两次取出的数字的和等于0的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大润发超市在销售某种进货价为20元/件的商品时,以30元/件售出,每天能售出100件.调查表明:这种商品的售价每上涨1元/件,其销售量就将减少2件.
(1)为了实现每天1600元的销售利润,超市应将这种商品的售价定为多少?
(2)设每件商品的售价为x元,超市所获利润为y元.
①求y与x之间的函数关系式;
②物价局规定该商品的售价不能超过40元/件,超市为了获得最大的利润,应将该商品售价定为多少?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月23日,是第23个世界读书日.为了推进中华传统文化教育,营造浓郁的读书氛围,我区某学校举办了“让读书成为习惯,让书香飘满校园”主题活动,为此,特为每个班级订购了一批新的图书.初一年级两个班订购图书情况如下表:
老舍文集(套) | 四大名著(套) | 总费用(元) | |
初一(1)班 | 2 | 2 | 330 |
初一(2)班 | 3 | 2 | 380 |

(1)求老舍文集和四大名著每套各多少元?
(2)学校准备再购买老舍文集和四大名著共10套,总费用超过500元而不超过800元,问学校有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2﹣4x+3与x轴交于A,B两点,其顶点为C.
(1)对于任意实数m,点M(m,﹣2)是否在该抛物线上?请说明理由;
(2)求证:△ABC是等腰直角三角形;
(3)若点D在x轴上,则在抛物线上是否存在点P,使得PD∥BC,且PD=BC?若存在,求点P的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com