[题目]将一矩形纸片沿一条直线剪成两个多边形.那么这两个多边形的内角和之和不可能是( )A.360°B.540°C.720°D.900° 题目和参考答案——青夏教育精英家教网—

【题目】将一矩形纸片沿一条直线剪成两个多边形，那么这两个多边形的内角和之和不可能是（　　）
A.360°
B.540°
C.720°
D.900°

【答案】D
【解析】解：①将矩形沿对角线剪开，得到两个三角形，两个多边形的内角和为：180°+180°=360°； ②将矩形从一顶点剪向对边，得到一个三角形和一个四边形，两个多边形的内角和为：180°+360°=540°；
③将矩形沿一组对边剪开，得到两个四边形，两个多边形的内角和为：360°+360°=720°；
故选：D．
根据题意列出可能情况，再分别根据多边形的内角和定理进行解答即可．本题考查了多边形的内角与外角，能够得出一个矩形截一刀后得到的图形有三种情形，是解决本题的关键．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图：已知在△ABC中，AB=AC，D为BC边的中点，过点D作DE⊥AB，DF⊥AC，垂足分别为E，F．
（1）求证：DE=DF；
（2）若∠A=60°，BE=1，求△ABC的周长．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知：⊙O上两个定点A，B和两个动点C，D，AC与BD交于点E．

（1）如图1，求证：EAEC=EBED；

（2）如图2，若，AD是⊙O的直径，求证：ADAC=2BDBC；

（3）如图3，若AC⊥BD，点O到AD的距离为2，求BC的长．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，抛物线与x轴交于点A，点B，与y轴交于点C，点B坐标为（6，0），点C坐标为（0，6），点D是抛物线的顶点，过点D作x轴的垂线，垂足为E，连接BD．

（1）求抛物线的解析式及点D的坐标；

（2）点F是抛物线上的动点，当∠FBA=∠BDE时，求点F的坐标；

（3）若点M是抛物线上的动点，过点M作MN∥x轴与抛物线交于点N，点P在x轴上，点Q在平面内，以线段MN为对角线作正方形MPNQ，请直接写出点Q的坐标．

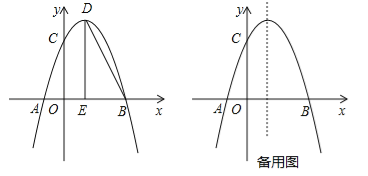
查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】下列事件中，是必然事件的是（　　）

A.经过有交通信号灯的路口，遇到红灯B.射击运动员射击一次，命中靶心

C.随意翻到一本书的某页，页码是奇数D.明天太阳从东方升起

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】八（3）班同学到野外上数学活动课，为测量池塘两端A、B的距离，设计了如下方案：
（Ⅰ）如图1，先在平地上取一个可直接到达A、B的点C，连接AC、BC，并分别延长AC至D，BC至E，使DC=AC，EC=BC，最后测出DE的距离即为AB的长；
（Ⅱ）如图2，先过B点作AB的垂线，再在BF上取C、D两点使BC=CD，接着过D作BD的垂线DE，交AC的延长线于E，则测出DE的长即为AB的距离．
阅读回答下列问题：

（1）方案（Ⅰ）是否可行？请说明理由．
（2）方案（Ⅱ）是否可行？请说明理由．
（3）方案（Ⅲ）中作BF⊥AB，ED⊥BF的目的是；若仅满足∠ABD=∠BDE≠90°，方案（Ⅱ）是否成立？．