
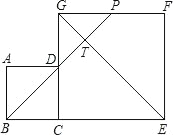
【题目】如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则GT的长为_____.
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】如图,现有一个均匀的转盘被平均分成6等份,分别标有数字2、3、4、5、6、7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字.

求:(1)转动转盘,转出的数字大于3的概率是多少?
(2)现有两张分别写有3和4的卡片,随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.
①这三条线段能构成三角形的概率是 .
②这三条线段能构成等腰三角形的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】袋子中装有2个红球,1个黄球,它们除颜色外其余都相同. 小明和小张做摸球游戏,约定一次游戏规则是:小张先从袋中任意摸出1个球记下颜色后放回,小明再从袋中摸出1个球记下颜色后放回,如果两人摸到的球的颜色相同,小张赢,否则小明赢.
(1)请用树状图或列表格法表示一次游戏中所有可能出现的结果;
(2)这个游戏规则对双方公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
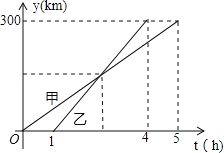
【题目】甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:①A,B两城相距300千米;②乙车比甲车晚出发1小时,却早到1小时; ③乙车出发后2小时追上甲车; ④当甲、乙两车相距50千米时,t=![]() 或
或![]() .其中正确的结论有_____.
.其中正确的结论有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
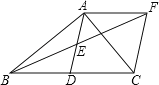
【题目】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
(1)求证:AD=AF;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新型冠状病毒肺炎疫情发生后,全社会积极参与疫情防控工作,某市为了尽快完成100万只口罩的生产任务,安排甲、乙两个大型工厂完成.已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的1.5倍,并且在独立完成60万只口罩的生产任务时,甲厂比乙厂少用5天.
(1)求甲、乙每天能生产多少万只口罩?
(2)问至少应安排两个工厂工作多少天才能完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
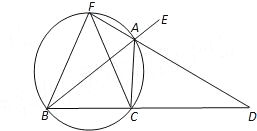
【题目】如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB、FC.
(1)求证:FB=FC;
(2)求证:FB2=FAFD;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】结合数轴与绝对值的知识回答下列问题:
![]()
(1)数轴上表示![]() 和
和![]() 的两点之间的距离是__________;表示
的两点之间的距离是__________;表示![]() 和
和![]() 两点之间的距离是__________;
两点之间的距离是__________;
(2)如果![]() ,那么
,那么![]() __________;
__________;
(3)若![]() ,
,![]() ,且数
,且数![]() 、
、![]() 在数轴上表示的点分别是点
在数轴上表示的点分别是点![]() 、点
、点![]() ,则
,则![]() 、
、![]() 两点间的最大距离是_____,最小距离是______;
两点间的最大距离是_____,最小距离是______;
(4)求代数式![]() 的最小值,并写出此时
的最小值,并写出此时![]() 可取哪些整数值?
可取哪些整数值?
(5)求代数式![]() 的最小值.
的最小值.
(6)若![]() 表示一个有理数,则代数式
表示一个有理数,则代数式![]() 有最大值吗?若有,请求出最大值;若没有,请说明理由.
有最大值吗?若有,请求出最大值;若没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com