解:(1)∵AB是⊙O的直径,⊙O过点C,
∴∠ACB=90°(直径所对的圆周角是直角).
(2)分两种情况讨论:

①C、D两点在直径AB异侧,连接BD,过B作BE⊥CD于E.
在△ABC中,∵∠ACB=90°,∠ABC=30°,AC=6,
∴AB=2AC=12,BC=

AC=6

.
∵在半圆AB上取中点D,
∴∠BCD=45°,
∴△BCE是等腰直角三角形,
∴BE=CE=

BC=3

.
在△BDE中,∵∠BED=90°,∠D=∠A=60°,
∴DE=

BE=3

,
∴CD=CE+DE=3

+3

;

②C、D两点在直径AB同侧,
连接BD,过B作BE⊥CD于E.
在△ABC中,∵∠ACB=90°,∠ABC=30°,AC=6,
∴AB=2AC=12,BC=

AC=6

.
∵在半圆AB上取中点D,
∴∠BCD=45°,
∴△BCE是等腰直角三角形,
∴BE=CE=

BC=3

.
在△BDE中,∵∠BED=90°,∠BDE=∠A=60°,
∴DE=

BE=3

,
∴CD=CE-DE=3

-3

.
故答案为:90,直径所对的圆周角是直角.
分析:(1)根据直径所对的圆周角是直角即可求出∠ACB的度数;
(2)分两种情况讨论:①C、D两点在直径AB异侧;②C、D两点在直径AB同侧.
点评:本题考查了圆周角定理,解直角三角形,作辅助线构造直角三角形及分类讨论是解题的关键.

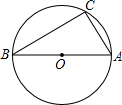 如图,在△ABC中,∠B=30°,以边AB的中点O为圆心,BO长为半径作⊙O,恰好过顶点C.在半圆AB上取点D,连接CD.
如图,在△ABC中,∠B=30°,以边AB的中点O为圆心,BO长为半径作⊙O,恰好过顶点C.在半圆AB上取点D,连接CD. ①C、D两点在直径AB异侧,连接BD,过B作BE⊥CD于E.
①C、D两点在直径AB异侧,连接BD,过B作BE⊥CD于E. AC=6
AC=6 .
. BC=3
BC=3 .
. BE=3
BE=3 ,
, +3
+3 ;
; ②C、D两点在直径AB同侧,
②C、D两点在直径AB同侧, AC=6
AC=6 .
. BC=3
BC=3 .
. BE=3
BE=3 ,
, -3
-3 .
.

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为