
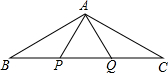
 已知:点P、Q是△ABC的边BC上的两个点,且BP=PQ=QC=AP=AQ,∠BAC的度数是( )
已知:点P、Q是△ABC的边BC上的两个点,且BP=PQ=QC=AP=AQ,∠BAC的度数是( )| A. | 100° | B. | 120° | C. | 130° | D. | 150° |
 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠ABC=30°,AB=p,BC=q,且p、q是关于x的方程x2-mx+3m=0的两个实数根,若|p+2q|=$\frac{1}{3}$pq+6,试在△ABC内找一点P,使P到A、B、C三点的距离之和最小,求出最小值并说明理由.
如图,在△ABC中,∠ABC=30°,AB=p,BC=q,且p、q是关于x的方程x2-mx+3m=0的两个实数根,若|p+2q|=$\frac{1}{3}$pq+6,试在△ABC内找一点P,使P到A、B、C三点的距离之和最小,求出最小值并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
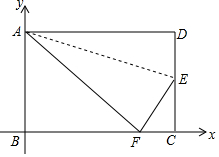 如图,矩形ABCD沿AE折叠,使D落在边BC上的F点处,若AB=8,BC=10以点B为坐标原点BC为x轴,AB为y轴,建立直角坐标系.
如图,矩形ABCD沿AE折叠,使D落在边BC上的F点处,若AB=8,BC=10以点B为坐标原点BC为x轴,AB为y轴,建立直角坐标系.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com