
【题目】如图,AB⊥BD,CD⊥MN,垂足分别是B、D点,∠FDC=∠EBA.
(1)判断CD与AB的位置关系;
(2)BE与DF平行吗?为什么?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】抛物线 ![]() 的图象先向右平移2个单位,再向下平移3个单位,所得图象的函数解析式为
的图象先向右平移2个单位,再向下平移3个单位,所得图象的函数解析式为 ![]() ,则b、c的值为( ).
,则b、c的值为( ).
A.b=2, c=-6
B.b=2, c=0
C.b=-6, c=8
D.b=-6, c=2
查看答案和解析>>
科目:初中数学 来源: 题型:
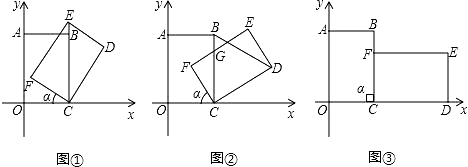
【题目】把边长分别为4和6的矩形ABCO如图放在平面直角坐标系中,将它绕点C顺时针旋转a角,旋转后的矩形记为矩形EDCF.在旋转过程中,
(1)如图①,当点E在射线CB上时,E点坐标为 ;
(2)当△CBD是等边三角形时,旋转角a的度数是 (a为锐角时);
(3)如图②,设EF与BC交于点G,当EG=CG时,求点G的坐标;
(4)如图③,当旋转角a=90°时,请判断矩形EDCF的对称中心H是否在以C为顶点,且经过点A的抛物线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(0,1),B(2,0),C(4,3).
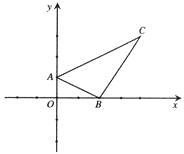
(1)求ΔABC的面积;
(2)设点P在坐标轴上,且ΔABP与ΔABC的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于矩形的说法,正确的是( )
A.对角线相等的四边形是矩形
B.对角线互相平分的四边形是矩形
C.矩形的对角线相等且互相平分
D.矩形的对角线互相垂直且平分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC交CD于E,DF平分∠ADC交AB于F.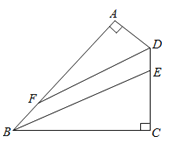
(1)若∠ABC=60°,则∠ADC= °,∠AFD=°;
(2)BE与DF平行吗?试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com