
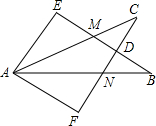
 如所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②AF∥EB;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的有________.
如所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②AF∥EB;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的有________.

科目:初中数学 来源: 题型:
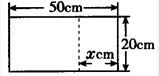 8、如所示,一长为50cm,宽为20cm的长方形木板,现要在长边上截去长为xcm的一部分,则剩余木板的面积S(cm)与x(0≤x<50)之间的关系式为( )
8、如所示,一长为50cm,宽为20cm的长方形木板,现要在长边上截去长为xcm的一部分,则剩余木板的面积S(cm)与x(0≤x<50)之间的关系式为( )查看答案和解析>>
科目:初中数学 来源: 题型:
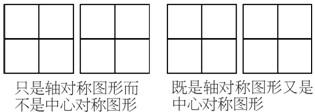
查看答案和解析>>
科目:初中数学 来源: 题型:
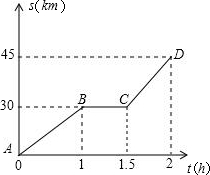 某人从甲地出发,骑摩托车去乙地,途中因车出现故障而停车修理,到达乙地时正好用了2h.已知摩托车行驶的路程s(km)与行驶的时间t(h)之间的函数关系如所示.若这辆摩托车平均每行驶100km的耗油量为2L,根据图中给出的信息,从甲地到乙地,这辆摩托车共耗油( )
某人从甲地出发,骑摩托车去乙地,途中因车出现故障而停车修理,到达乙地时正好用了2h.已知摩托车行驶的路程s(km)与行驶的时间t(h)之间的函数关系如所示.若这辆摩托车平均每行驶100km的耗油量为2L,根据图中给出的信息,从甲地到乙地,这辆摩托车共耗油( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com