
【题目】二次函数![]() 的部分图象如图,图象过点(﹣1,0),对称轴为直线
的部分图象如图,图象过点(﹣1,0),对称轴为直线![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④当
;④当![]() 时,
时, ![]() 随
随![]() 的增大而增大.其中正确的结论有( )
的增大而增大.其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
科目:初中数学 来源: 题型:
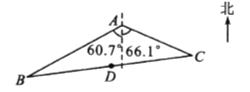
【题目】如图,湿地景区岸边有三个观景台![]() 、
、![]() 、
、![]() .已知
.已知![]() m,
m, ![]() m,点
m,点![]() 位于点
位于点![]() 的南偏西60. 7°方向,点
的南偏西60. 7°方向,点![]() 位于点
位于点![]() 的南偏东66. 1°方向.
的南偏东66. 1°方向.
(1)求![]() 的面积;
的面积;
(2)景区规划在线段![]() 的中点
的中点![]() 处修建一个湖心亭,并修建观景栈道
处修建一个湖心亭,并修建观景栈道![]() .试求
.试求![]() 、
、![]() 间的距离.(结果精确到0. 1 m,参考数据:
间的距离.(结果精确到0. 1 m,参考数据: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设![]() =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;
(3)当∠ABE的正切值是![]() 时,求AB的长.
时,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题
(1)计算:﹣32÷(﹣3)2+3×(﹣2)+|﹣4|
(2)计算:![]()
(3)化简:(5a2+2a﹣1)﹣4[3﹣2(4a+a2)]
(4)化简:3x2﹣[7x﹣(4x﹣3)﹣2x2]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1为某月的月历表,图2是![]() 型的框图,且框图中五个小正方形与月历表中每个小正方形大小相同.观察并思考下列问题:
型的框图,且框图中五个小正方形与月历表中每个小正方形大小相同.观察并思考下列问题:
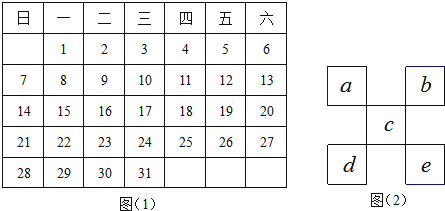
(1)用图2框图在月历表中任意圈出5个数(日期),这5个数的和的最小值是 ,最大值是 .
(2)在该月历表中可以得到 个这样的框图;
(3)如果型框图中5个数的和为80,则图二中字母a代表的数字是多少?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E、F分别是ABCD的边BC、AD上的点,且BE=DF.

(1)试判断四边形AECF的形状;
(2)若AE=BE,∠BAC=90°,求证:四边形AECF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一顶点重合的两个大小完全相同的边长为3的正方形ABCD和正方形AB′C′D′,如图所示,∠DAD′=45°,边BC与D′C′交于点O,则四边形ABOD′的周长是( )

A. 6 B. 6![]() C. 3
C. 3![]() D. 3+3
D. 3+3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,在矩形纸片
,在矩形纸片![]() 中,
中,![]() ,
,![]() ,折叠纸片使
,折叠纸片使![]() 点落在边
点落在边![]() 上的
上的![]() 处,折痕为
处,折痕为![]() .过点
.过点![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
(1)求证:四边形![]() 为菱形;
为菱形;
(2)当点![]() 在
在![]() 边上移动时,折痕的端点
边上移动时,折痕的端点![]() ,
,![]() 也随之移动.
也随之移动.
①当点![]() 与点
与点![]() 重合时(如图
重合时(如图![]() ),求菱形
),求菱形![]() 的边长;
的边长;
②若限定![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上移动,求出点
上移动,求出点![]() 在边
在边![]() 上移动的最大距离.
上移动的最大距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
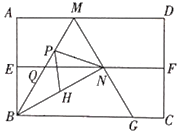
【题目】如图,四边形是矩形纸片,AB=2.对折矩形纸片ABCD,使AD与BC重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q再次展平,连接BN,MN,延长MN交BC于点G.有如下结论:①∠ABN= 60°;②AM=1;③![]() ;④△BMG是等边三角形;⑤P为线段BM上一动点,H是BN的中点,则PN+PH的最小值是
;④△BMG是等边三角形;⑤P为线段BM上一动点,H是BN的中点,则PN+PH的最小值是![]() .其中正确结论的序号是___________.
.其中正确结论的序号是___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com