
分析 (1)根据题意可以用相应的代数式表示出未出租的电器设备数(套)和所有未出租电器设备(套)的支出费用;
(2)根据题意可以表示出y与x之间的二次函数表达式;
(3)根据(2)中函数解析式可以写出该函数的顶点式,以及求出函数的最值.
解答 解:(1)由题意可得,
未出租的电器设备数(套)是:$\frac{x-50}{10}$套,
所有未出租电器设备(套)的支出费用(元)是:$\frac{x-50}{10}×20$=(2x-100)元;
(2)由题意可得,
y=x(10-$\frac{x-50}{10}$)-(2x-100)=$-\frac{1}{10}{x}^{2}+13x+100$,
即y与x之间的二次函数表达式是y=$-\frac{1}{10}{x}^{2}+13x+100$;
(3)∵y=$-\frac{1}{10}{x}^{2}+13x+100$=$-\frac{1}{10}(x-65)^{2}+522.5$,
∵x取10的整数倍,
∴当x=60或x=70时,y取得最大值,此时y=520,
即当x为60或70时,租赁公司出租该型号电器设备的月收益最大,最大月收益是520元.
点评 本题考查二次函数的应用,解答此类题目的关键是明确题意,找出所求问题题目需要的条件,注意要联系实际情况,x取10的整数倍,为租出的机器数才是整数,这也是易错点.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
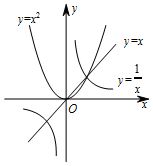 给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象
给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象| A. | 正确的命题是①④ | B. | 错误的命题是②③④ | C. | 正确的命题是①② | D. | 错误的命题只有③ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com