
【题目】货车和轿车分别从甲、乙两地同时出发,沿同一公路相向而行.轿车出发2.4h后休息,直至与货车相遇后,以原速度继续行驶.设货车出发xh后,货车、轿车分别到达离甲地y1km和y2km的地方,图中的线段OA、折线BCDE分别表示y1、y2与x之间的函数关系.
(1)求点D的坐标,并解释点D的实际意义;
(2)求线段DE所在直线的函数表达式;
(3)当货车出发________h时,两车相距200km.
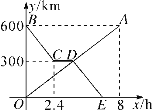
【答案】(1) (4,300),货车出发4h后,与轿车在距离A地300km处相遇; (2) y=-125x+800; (3) 2或5
【解析】
(1)待定系数法求出![]() 的解析式,再根据点
的解析式,再根据点![]() 的纵坐标为300求得其横坐标,即可得解;
的纵坐标为300求得其横坐标,即可得解;
(2)轿车在休息前![]() 行驶
行驶![]() ,休息后按原速度行驶,可得轿车行驶后
,休息后按原速度行驶,可得轿车行驶后![]() 需
需![]() ,从而可得点
,从而可得点![]() 的坐标,再结合点
的坐标,再结合点![]() 的坐标,用待定系数法可求得答案;
的坐标,用待定系数法可求得答案;
(3)先用待定系数法求出![]() 段的解析式,然后分两种情况列方程求解即可:①当轿车休息前与货车相距200km时;②当轿车休息后与货车相距200km时.
段的解析式,然后分两种情况列方程求解即可:①当轿车休息前与货车相距200km时;②当轿车休息后与货车相距200km时.
解:(1)设OA所在直线解析式为y=mx,
将A(8,600)代入,得600=8m,解得m=75,
∴OA所在直线的解析式为y=75x.
令y=300,得75x=300,解得x=4,
∴点D坐标为(4,300),其实际意义为货车出发4h后,与轿车在距离A地300km处相遇.
故答案为:点D坐标为(4,300),其实际意义为货车出发4h后,与轿车在距离A地300km处相遇.
(2)由图象知,轿车在休息前2.4h行驶距离为300km,
休息后按原速度行驶,
∴轿车行驶后![]() 需
需![]() ,
,
又因为点![]() 坐标为
坐标为![]() ,
,
故点E坐标为(6.4,0),
设线段![]() 所在直线的函数表达式为
所在直线的函数表达式为![]()
将点![]() ,
,![]() 代入得:
代入得:![]()
解得![]()
![]() 线段
线段![]() 所在直线的函数表达式为
所在直线的函数表达式为![]() ;
;
(3)2或5
设![]() 段的函数解析式为
段的函数解析式为![]()
将![]() ,
,![]() 代入得:
代入得:![]()
解得:![]()
![]()
①当轿车休息前与货车相距200km时,有-125x+600-75x=200,解得x=2;
②当轿车休息后与货车相距200km时,有75x-(-125x+800)=200,解得x=5.
故答案为:2或5.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=mx2﹣2mx﹣3m与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,连接AC,BC,将△OBC沿BC所在的直线翻折,得到△DBC,连接OD.
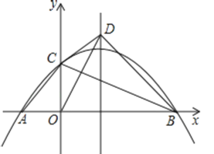
(1)点A的坐标为 ,点B的坐标为 .
(2)如图,若点D落在抛物线的对称轴上,且在x轴上方,求抛物线的解析式.
(3)设△OBD的面积为S1,△OAC的面积为S2,若S1=![]() S2,求m的值.
S2,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 是
是![]() 的内接四边形,四边形
的内接四边形,四边形![]() 两组对边的延长线分别相交于点
两组对边的延长线分别相交于点![]() ,
,![]() ,且
,且![]() ,
,![]() ,连接
,连接![]() .
.

(1)求![]() 的度数;
的度数;
(2)当![]() 的半径等于2时,请直接写出
的半径等于2时,请直接写出![]() 的长.(结果保留
的长.(结果保留![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
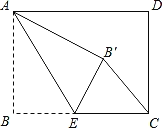
【题目】如图,长方形ABCD中,AB=3,BC=4,点E是BC边上任一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当CE的长为_____时,△CEB′恰好为直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
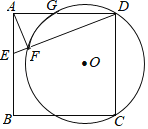
【题目】如图,正方形ABCD中,E为AB上一点,AF⊥DE于点F,已知DF=5EF=5,过C、D、F的⊙O与边AD交于点G,则DG=( )
A.2![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,与三角形各边都相切的圆叫做三角形的内切圆,则三角形可以称为圆的外切三角形.如图1,![]() 与
与![]() 的三边
的三边![]() 分别相切于点
分别相切于点![]() 则
则![]() 叫做
叫做![]() 的外切三角形.以此类推,各边都和圆相切的四边形称为圆外切四边形.如图2,
的外切三角形.以此类推,各边都和圆相切的四边形称为圆外切四边形.如图2,![]() 与四边形ABCD的边
与四边形ABCD的边![]() 分别相切于点
分别相切于点![]() 则四边形
则四边形![]() 叫做
叫做![]() 的外切四边形.
的外切四边形.
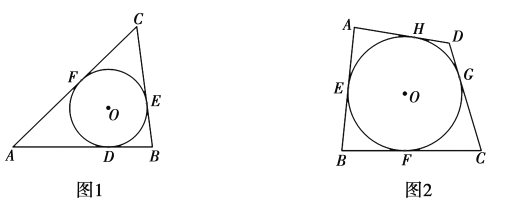
(1)如图2,试探究圆外切四边形![]() 的两组对边
的两组对边![]() 与
与![]() 之间的数量关系,猜想:
之间的数量关系,猜想:![]()
![]() (横线上填“>”,“<”或“=”);
(横线上填“>”,“<”或“=”);
(2)利用图2证明你的猜想(写出已知,求证,证明过程);
(3)用文字叙述上面证明的结论: ;
(4)若圆外切四边形的周长为![]() 相邻的三条边的比为
相邻的三条边的比为![]() ,求此四边形各边的长.
,求此四边形各边的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
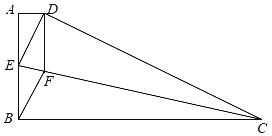
【题目】如图,四边形ABCD中,AD//BC,∠A=90°,CD=CB,过点C作∠DCB的平分线CE交AB于点E,连接DE,过点D作DF//AB,且交CE于F点,连接BF.
(1)求证:四边形DEBF是菱形;
(2)若AB=5,BC=13,求tan∠AED的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com