

科目:初中数学 来源:不详 题型:单选题
 和
和 . 现给出下列命题:
. 现给出下列命题:
 ,则
,则 ;②若
;②若 ,则DF=2AD.
,则DF=2AD.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的方向运动,且点P与点B,A都不重合.图2是此运动过程中,△ABP的面积
的方向运动,且点P与点B,A都不重合.图2是此运动过程中,△ABP的面积 与点P经过的路程
与点P经过的路程 之间的函数图象的一部分.
之间的函数图象的一部分.
 =________,
=________, =________;
=________; 时,
时, 与
与 之间的函数关系式是__________________
之间的函数关系式是__________________ 与
与 的函数图象补充完整.
的函数图象补充完整.
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.12 | B.9 | C.8 | D.5 |
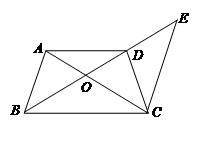
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
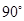 ,∠C=
,∠C=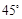 ,AD=1,BC=4,点E为AB中点,EF∥DC交BC于点F,求EF的长。
,AD=1,BC=4,点E为AB中点,EF∥DC交BC于点F,求EF的长。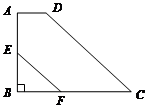

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题


 如不能成功,请说明理由
如不能成功,请说明理由查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com