
【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,PF∥BC交AB于F,连接PQ交AB于D.
(1)当∠BQD=30°时,求AP的长;
(2)当运动过程中线段ED的长始终保持不变,试求出ED的长度.

【答案】(1)2;(2)3.
【解析】
试题分析:(1)由△ABC是边长为6的等边三角形,可知∠ACB=60°,再由∠BQD=30°可知∠QPC=90°,设AP=x,则PC=6﹣x,QB=x,在Rt△QCP中,∠BQD=30°,PC=![]() QC,即6﹣x=
QC,即6﹣x=![]() (6+x),求出x的值即可;
(6+x),求出x的值即可;
(2)作QG⊥AB,交直线AB于点G,连接QE,PG,由点P、Q做匀速运动且速度相同,可知AP=BQ,再根据全等三角形的判定定理得出△APE≌△BQG,再由AE=BG,PE=QG且PE∥QG,可知四边形PEQG是平行四边形,进而可得出EB+AE=BE+BG=AB,DE=![]() AB,由等边△ABC的边长为6,可得出DE=3.
AB,由等边△ABC的边长为6,可得出DE=3.
试题解析:(1)∵△ABC是边长为6的等边三角形,∴∠ACB=60°,∵∠BQD=30°,∴∠QPC=90°,设AP=x,则PC=6﹣x,QB=x,∴QC=QB+BC=6+x,∵在Rt△QCP中,∠BQD=30°,∴PC=![]() QC,即6﹣x=
QC,即6﹣x=![]() (6+x),解得x=2,∴AP=2;(2)作QG⊥AB,交直线AB于点G,连接QE,PG,又∵PE⊥AB于E,∴∠DGQ=∠AEP=90°,∵点P、Q速度相同,∴AP=BQ,∵△ABC是等边三角形,∴∠A=∠ABC=∠GBQ=60°,在△APE和△BQG中,∵∠AEP=∠BGQ=90°,
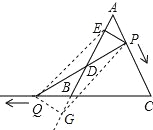
(6+x),解得x=2,∴AP=2;(2)作QG⊥AB,交直线AB于点G,连接QE,PG,又∵PE⊥AB于E,∴∠DGQ=∠AEP=90°,∵点P、Q速度相同,∴AP=BQ,∵△ABC是等边三角形,∴∠A=∠ABC=∠GBQ=60°,在△APE和△BQG中,∵∠AEP=∠BGQ=90°,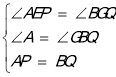 ,∴△APE≌△BQG(AAS),∴AE=BG,PE=QG且PE∥QG,∴四边形PEQG是平行四边形,∴DE=
,∴△APE≌△BQG(AAS),∴AE=BG,PE=QG且PE∥QG,∴四边形PEQG是平行四边形,∴DE=![]() EG,∵EB+AE=BE+BG=AB=EG,∴DE=
EG,∵EB+AE=BE+BG=AB=EG,∴DE=![]() AB,又∵等边△ABC的边长为6,∴DE=3,故运动过程中线段ED的长始终为3.
AB,又∵等边△ABC的边长为6,∴DE=3,故运动过程中线段ED的长始终为3.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 一个三角形中至少有一个角不大于60° B. 锐角三角形中任意两个角的和小于直角
C. 一个三角形中至多有一个角是钝角 D. 一个三角形中至多有一个角是直角
查看答案和解析>>
科目:初中数学 来源: 题型:
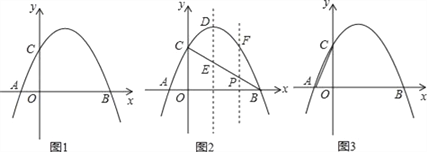
【题目】如图1,抛物线y=﹣x2+2x+3与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C.
(1)直接写出A、B、C三点的坐标和抛物线的对称轴;
(2)如图2,连接BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m;用含m的代数式表示线段PF的长;并求出当m为何值时,四边形PEDF为平行四边形?
(3)如图3,连接AC,在x轴上是否存在点Q,使△ACQ为等腰三角形,若存在,请求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
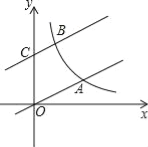
【题目】如图,直线y=![]() x与双曲线y=
x与双曲线y=![]() (k>0,x>0)交于点A,将直线y=
(k>0,x>0)交于点A,将直线y=![]() x向上平移4个单位长度后,与y轴交于点C,与双曲线y=
x向上平移4个单位长度后,与y轴交于点C,与双曲线y=![]() (k>0,x>0)交于点B.若OA=3BC,则k的值为 .
(k>0,x>0)交于点B.若OA=3BC,则k的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com