
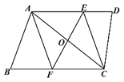
【题目】如图,在四边形ABCD中,AD∥BC,点O是对角线AC的中点,过点O作AC的垂线,分别交AD、BC于点E、F,连接AF、CE.试判断四边形AECF的形状,并证明.
科目:初中数学 来源: 题型:
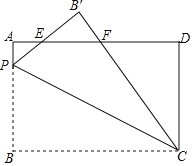
【题目】如图,矩形ABCD中,AB=5,BC=8,点P在AB上,AP=1.将矩形ABCD沿CP折叠,点B落在点B'处.B'P、B′C分别与AD交于点E、F,则EF=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M,N是以AB为直径的⊙O上的点,且![]() =
=![]() ,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
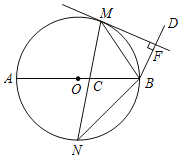
(1)求证:MF是⊙O的切线;
(2)若CN=3,BN=4,求CM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
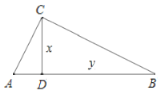
【题目】如图,在![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,
,![]() ,为了研究图中线段之间的关系,设
,为了研究图中线段之间的关系,设![]() ,
,![]() ,
,
(1)可通过证明![]() ,得到
,得到![]() 关于
关于![]() 的函数表达式
的函数表达式![]() __________,其中自变量
__________,其中自变量![]() 的取值范围是___________;
的取值范围是___________;
(2)根据图中给出的(1)中函数图象上的点,画出该函数的图象;

(3)借助函数图象,回答下列问题:①![]() 的最小值是__________;②已知当
的最小值是__________;②已知当![]() 时,
时,![]() 的形状与大小唯一确定,借助函数图象给出
的形状与大小唯一确定,借助函数图象给出![]() 的一个估计值(精确到0.1)或者借助计算给出
的一个估计值(精确到0.1)或者借助计算给出![]() 的精确值.
的精确值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,B,与反比例函数图象的一个交点为
,B,与反比例函数图象的一个交点为![]() .
.
(1)求反比例函数的表达式;
(2)设直线![]() 与
与![]()
![]() 轴,
轴,![]() 轴分别交于点C,D,且
轴分别交于点C,D,且![]() ,直接写出
,直接写出![]() 的值 .
的值 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学分别进行6次射击训练,训练成绩(单位:环)如下表
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六交 | |
甲 | 9 | 8 | 6 | 7 | 8 | 10 |
乙 | 8 | 7 | 9 | 7 | 8 | 8 |
对他们的训练成绩作如下分析,其中说法正确的是( )
A. 他们训练成绩的平均数相同 B. 他们训练成绩的中位数不同
C. 他们训练成绩的众数不同 D. 他们训练成绩的方差不同
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在反比例函数![]() 的图象上,点C,D在反比例函数
的图象上,点C,D在反比例函数![]() 的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为
的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为![]() ,则k的值为( )
,则k的值为( )

A. 4 B. 3 C. 2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
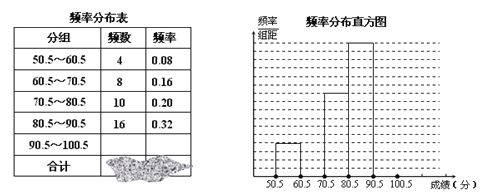
【题目】为了让学生了解环保知识,增强环保意识,红星中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
(1)填充频率分布表中的空格;
(2)补全频率分布直方图;
(3)在该问题中的样本容量是多少?
答: .
(4)全体参赛学生中,竞赛成绩落在哪组范围内的人数最多?(不要求说明理由)”
答: .
(5)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为多少人?
答: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学图书室计划购买了甲、乙两种故事书.若购买7本甲种故事书和4本乙种故事书需510元;购买3本甲种故事书和5本乙种故事书需350元.
(1)求甲种故事书和乙种故事书的单价;
(2)学校准备购买甲、乙两种故事书共200本,且甲种故事书的数量不少于乙种故事书的数量的![]() ,请设计出最省钱的购买方案,并说明理由.
,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com