
 如图,两个扇形半径均为1,α=120°,β=60°,则大扇形与小扇形的面积之差为$\frac{π}{6}$.
如图,两个扇形半径均为1,α=120°,β=60°,则大扇形与小扇形的面积之差为$\frac{π}{6}$. 分析 利用扇形的面积公式分别求出两个扇形的面积,再用较大面积减去较小的面积即可.
解答 解:$\frac{(360°-60°)π×{1}^{2}}{360°}$-$\frac{(360°-120°)π×{1}^{2}}{360°}$
=$\frac{5}{6}$π-$\frac{2}{3}$π
=$\frac{π}{6}$.
答:大扇形与小扇形的面积之差为$\frac{π}{6}$.
故答案为:$\frac{π}{6}$.
点评 此题主要考查了扇形的面积公式,熟记扇形的面积公式扇形面积计算公式:设圆心角是n°,圆的半径为R的扇形面积为S,则S扇形=$\frac{nπ{r}^{2}}{360°}$πR2或S扇形=$\frac{1}{2}$lR(其中l为扇形的弧长)是解答此题的关键.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
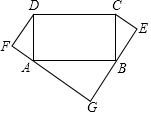 如图,矩形ABCD中,AD=5,AB=10,分别以AD、BC为斜边向矩形外作Rt△ADF≌Rt△CBE,延长FA、EB交于点G.
如图,矩形ABCD中,AD=5,AB=10,分别以AD、BC为斜边向矩形外作Rt△ADF≌Rt△CBE,延长FA、EB交于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
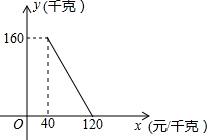 某商店以40元/千克的单价新进一批茶叶,经调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的函数关系如图所示
某商店以40元/千克的单价新进一批茶叶,经调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的函数关系如图所示查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2x-xy=5 | B. | $\frac{x}{2}$+3y=1 | C. | x+$\frac{1}{y}$=2 | D. | x2-2y=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com