
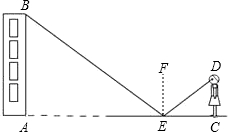
 小强在地面E处放一面镜子,刚好能从镜子中看到教学楼的顶端B,此时EA=21米,CE=2.5米.已知眼睛距离地面的高度DC=1.6米,请计算出教学楼的高度.(根据光的反射定律,反射角等于入射角)
小强在地面E处放一面镜子,刚好能从镜子中看到教学楼的顶端B,此时EA=21米,CE=2.5米.已知眼睛距离地面的高度DC=1.6米,请计算出教学楼的高度.(根据光的反射定律,反射角等于入射角) 分析 根据反射角等于入射角可得∠AEB=∠CED,则可判断Rt△AEB∽Rt△CED,根据相似三角形的性质得$\frac{AB}{1.6}$=$\frac{21}{2.5}$,然后利用比例性质求出AB即可.
解答 解:根据题意得∠AEB=∠CED,
∵Rt△AEB∽Rt△CED,
∴$\frac{AB}{CD}$=$\frac{AE}{CE}$,即$\frac{AB}{1.6}$=$\frac{21}{2.5}$,
解得:AB=13.44.
答:教学楼的高度为13.44m.
点评 本题考查了相似三角形的应用:利用入射与反射构造相似三角形,然后利用相似三角形的性质即相似三角形的对应边的比相等解决问题.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:解答题
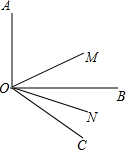 如图,OB是∠AOC内的一条射线,OM平分∠AOC,ON平分∠BOC,其中∠BOC是锐角.
如图,OB是∠AOC内的一条射线,OM平分∠AOC,ON平分∠BOC,其中∠BOC是锐角.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将长方形ABCD沿AE折叠,使点D落在BC边上的点F,若∠BAF=60°,则∠DAE=( )
如图,将长方形ABCD沿AE折叠,使点D落在BC边上的点F,若∠BAF=60°,则∠DAE=( )| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
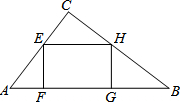 如图,在Rt△ABC中,∠ACB=90°,AB=10,sinB=$\frac{3}{5}$,点E在边AC上,过点E作EF⊥AB交AB于点F,EH∥AB交BC于点H,边点H作HG⊥AB于点G,设EF=x.
如图,在Rt△ABC中,∠ACB=90°,AB=10,sinB=$\frac{3}{5}$,点E在边AC上,过点E作EF⊥AB交AB于点F,EH∥AB交BC于点H,边点H作HG⊥AB于点G,设EF=x.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com