Question

某公司专销产品A，第一批产品A上市40天内全部售完．该公司对第一批产品A上市后市场销售情况进行了跟踪调查，调查结果如图所示：其中，图①中的折线表示的是市场日销售量与上市时间的关系，图②中的折线表示的是每件产品A的销售利润与上市时间的关系．
（1）试写出第一批产品A的市场日销售量y与上市时间t的关系式；试写出第一批产品A，每件销售利润p与上市时间t的关系式；
（2）这家公司在第35天的市场日销售利利润是多少万元？

Answer 1

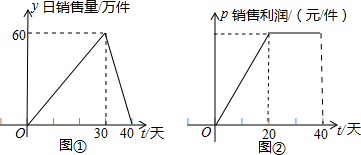
解：（1）由图①可得，
当0≤t≤30时，设市场的日销售量y=kt，
∵点（30，60）在图象上，∴60=30k，
∴k=2，即y=2t；
当30＜t≤40时，设市场的日销售量y=k₁t+b，
∵点（30，60）和（40，0）在图象上，
∴，
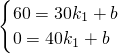
解得k₁=-6，b=240．
∴y=-6t+240．
综上可知，当0≤t≤30时，市场的日销售量y=2t；
当30＜t≤40时，市场的日销售量y=-6t+240．
由图②可得：
当0≤t≤20时，每件产品的日销售利润为P=3t；
当20＜t≤40时，每件产品的日销售利润为P=60．

（2）当t=35时，W=（-6×35+240）×60=1800，
∴在第35天时，日销售利润是1800万元﹒
分析：（1）市场日销售量y与上市时间t，每件销售利润p与上市时间t这两个函数都为分段函数，当t≤30时，设一次函数为y=kt，将点（30，60）代入可将此函数关系式表示出来；当30＜t≤40时，设一次函数为y=k₁t+b，将点（30，60），（40，0）代入进行求解，可将日销售量y与上市时间t的关系式写出；同理可求出销售利润p与上市时间t的函数关系式；
（2）由（1）中的关系式，把x=35代入W=60（-6t+240）中即可求出答案．
点评：本题考查了一次函数的实际应用，难度不大，注意所求函数是分段函数，要分段讨论．
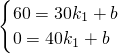