
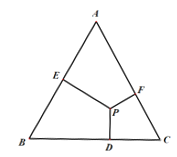
【题目】如图,在边长为2的正三角形ABC中,已知点P是三角形内任意一点,则点P到三角形三边距离之和PD+PE+PF的值是______.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于给定的两点
中,对于给定的两点![]() ,
,![]() ,若存在点
,若存在点![]() ,使得
,使得![]() 的面积等于1,即
的面积等于1,即![]() ,则称点
,则称点![]() 为线段
为线段![]() 的“单位面积点”.
的“单位面积点”.
解答下列问题:
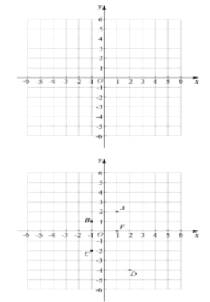
如图,在平面直角坐标系![]() 中,点
中,点![]() 的坐标为
的坐标为![]() .
.
(1)在点![]() ,
,![]() ,
,![]() ,
,![]() 中,线段
中,线段![]() 的“单位面积点”是______.
的“单位面积点”是______.
(2)已知点![]() ,
,![]() ,点
,点![]() ,
,![]() 是线段
是线段![]() 的两个“单位面积点”,点
的两个“单位面积点”,点![]() 在
在![]() 的延长线上,若
的延长线上,若![]() ,直接写出点
,直接写出点![]() 纵坐标的取值范围.
纵坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料,并按要求完成相应的任务.
课题学习:如何解一元二次不等式?
例题:解一元二次不等式![]() .
.
解:![]()
![]() .
.
由有理数的乘法法则“两数相乘,同号得正”,有:
![]()
![]()
解不等式组![]() 得:
得:![]()
解不等式组![]() 得:
得:![]()
![]() 的解集为
的解集为![]() 或
或![]() .
.
即:一元二次不等式![]() 的解集为
的解集为![]() 或
或![]() .
.
任务:(1)上面解一元二次不等式的过程中体现出了数学的一些基本思想方法,请在下列选项中选出你认为正确的一项:_____ ;(填选项即可)
A.分类讨论思想;B.数形结合思想;C.公理化思想;D.函数思想
(2)求一元二次不等式![]() 的解集为:_____ ;(直接填写结果,不写解答过程)
的解集为:_____ ;(直接填写结果,不写解答过程)
(3)仿照例题中的数学思想方法,求分式不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
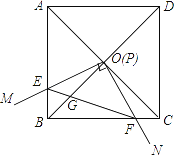
【题目】如图,边长为1的正方形ABCD的对角线AC、BD相交于点O,有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是________.
(1)EF=![]() OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)BE+BF=
OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)BE+BF= ![]() OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=
OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小米手机越来越受到大众的喜爱,各种款式相继投放市场,某店经营的A款手机去年销售总额为50000元,今年每部销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少![]() .
.
A,B两款手机的进货和销售价格如下表:
A款手机 | B款手机 | |
进货价格 | 1100 | 1400 |
销售价格 | 今年的销售价格 | 2000 |
(1)今年A款手机每部售价多少元?
(2)该店计划新进一批A款手机和B款手机共60部,且B款手机的进货数量不超过A款手机数量的两倍,应如何进货才能使这批手机获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),将一个长为4a,宽为2b的长方形,沿图中虚线均匀分成4个小长方形,然后按图(2)形状拼成一个正方形.
①图(2)中的空白部分的边长是多少?(用含a,b的式子表示)
②观察图(2),用等式表示出![]() ,ab和
,ab和![]() 的数量关系;
的数量关系;

(2)如图所示,在△ABC与△DCB中,AC与BD相交于点E,且∠A=∠D,AB=DC.求证:△ABE≌△DCE;

查看答案和解析>>
科目:初中数学 来源: 题型:
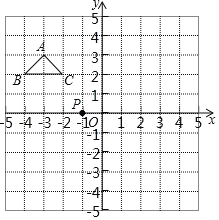
【题目】如图,在建立平面直角坐标系的网格纸中,每个小方格都是边长为1个单位长度的小正方形,△ABC的顶点均在格点上,点P的坐标为(-1,0).
(1)把△ABC绕点P旋转180°得到△A’B’C’,作出△A’B’C’;
(2)把△ABC向右平移7个单位长度得到△A″B″C″,作出△A″B″C″;
(3)△A’B’C’与△A″B″C″是否成中心对称?若是,则找出对称中心P’,并写出其坐标;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人共同计算一道整式乘法题:(2x+a)(3x+b).甲由于把第一个多项式中的“+a”看成了“﹣a”,得到的结果为6x2+11x﹣10;乙由于漏抄了第二个多项式中x的系数,得到的结果为2x2﹣9x+10.
(1)求a、b的值.
(2)计算这道乘法题的正确结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
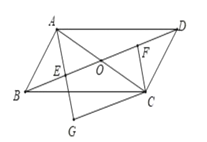
【题目】如图,在ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点延长AE至G,使EG=AE,连接CG.
(1)求证:△ABE≌△CDF;
(2)当AB=![]() AC时,判断四边形EGCF是什么形状?请说明理由.
AC时,判断四边形EGCF是什么形状?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com