Question

如右图，已知B、F、E、D在一直线上，AB=CD，∠B=∠D，BF=DE。

求证`：（1）AE=CF；（2）∠AFE=∠CEF。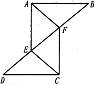

 

Answer 1

答案：
解析：

证明：（1）∵BF=DE，         ∴BF+EF=DE+EF，即BE=DF， ∵AB=CD，∠B=∠D，BE=DR， ∴△AEB≌△CFD（SAS）。 ∴AE=CF。 （2）由（1）得△AEB≌△CFD， ∴∠AFE=∠CEF。 ∵AE=CF，∠AFE=∠CEF，EF=FE， ∴△AEF≌△CFE （SAS） ∴∠AFE=∠CEF。

提示：

要证AE=CF，考察已知条件，可设法通过证明△AEB与△CFD全等来实现。证明的关键是将判断△AEB与△CFD全等的间接条件（BF=DE）转化为直接条件（BE=DF），（2）中证明出∠AFE=∠CEF，可行AE∥CF，所以∠AFE=∠CEF。