
 如图,△ABC的中线BD、CE相交于点O,OF⊥BC,且AB=6,BC=5,AC=3,OF=2,则四边形ADOE的面积是5.
如图,△ABC的中线BD、CE相交于点O,OF⊥BC,且AB=6,BC=5,AC=3,OF=2,则四边形ADOE的面积是5. 分析 首先根据三角形的面积=底×高÷2,求出△BOC的面积是多少;然后根据三角形的中线将三角形分成面积相等的两部分,可得△BCD、△ACE的面积均是△ABC的面积的一半,据此判断出四边形ADOE的面积等于△BOC的面积,据此解答即可.
解答 解:∵BD、CE均是△ABC的中线,
∴S△BCD=S△ACE=$\frac{1}{2}$S△ABC,
∴S四边形ADOE+S△COD=S△BOC+S△COD,
∴S四边形ADOE=S△BOC=5×2÷2=5.
故答案为:5.
点评 此题主要考查了三角形的面积的求法,以及三角形的中线的性质,要熟练掌握,解答此题的关键要明确:(1)三角形的中线将三角形分成面积相等的两部分;(2)三角形的面积=底×高÷2.


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=ax+1(a≠0)与x轴交于点A,与y轴交于点B,与双曲线y=$\frac{k}{x}$在第四象限的交点为C.若点B与点C关于点A对称,且△BOC的面积为$\sqrt{3}$.
如图,直线y=ax+1(a≠0)与x轴交于点A,与y轴交于点B,与双曲线y=$\frac{k}{x}$在第四象限的交点为C.若点B与点C关于点A对称,且△BOC的面积为$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
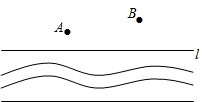 如图,政府决定实施“引河入村”的工程,需将河水经A村引入B村,要使修渠路线最短,水泵站的位置P应建在河边的什么地方,并画出水渠的修建路线.
如图,政府决定实施“引河入村”的工程,需将河水经A村引入B村,要使修渠路线最短,水泵站的位置P应建在河边的什么地方,并画出水渠的修建路线.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com