
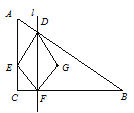
°æƒø°ø»ÁÕº£¨°˜ABC÷–£¨°œC£Ω90°„£¨AC£Ω3cm£¨BC£Ω4cm£¨µ„E°¢FÕ¨ ±¥”µ„C≥ˆ∑¢£¨“‘![]() cm/sµƒÀŸ∂»∑÷±—ÿCA°¢CB‘»ÀŸ‘À∂Ø£¨µ±µ„EµΩ¥Ôµ„ A ±£¨¡Ωµ„Õ¨ ±Õ£÷π‘À∂Ø£¨…Ë‘À∂Ø ±º‰Œ™ts£Æπ˝µ„F◊˜BCµƒ¥πœþlΩªAB”⁄µ„D£¨µ„G”ε„Eπÿ”⁄÷±œþl∂‘≥∆£Æ
cm/sµƒÀŸ∂»∑÷±—ÿCA°¢CB‘»ÀŸ‘À∂Ø£¨µ±µ„EµΩ¥Ôµ„ A ±£¨¡Ωµ„Õ¨ ±Õ£÷π‘À∂Ø£¨…Ë‘À∂Ø ±º‰Œ™ts£Æπ˝µ„F◊˜BCµƒ¥πœþlΩªAB”⁄µ„D£¨µ„G”ε„Eπÿ”⁄÷±œþl∂‘≥∆£Æ
£®1£©µ±t £Ω s ±£¨µ„G‘⁄°œABCµƒ∆Ω∑÷œþ…œ£ª
£®2£©µ±t £Ω s ±£¨µ„G‘⁄AB±þ…œ£ª
£®3£©…Ë°˜DFG”ΰ˜DFB÷ÿ∫œ≤ø∑÷µƒ√ʪ˝Œ™Scm2£¨ «ÛS”Ît÷ƺ‰µƒ∫Ø ˝πÿœµ Ω£¨≤¢–¥≥ˆtµƒ»°÷µ∑∂Œß£Æ

°æ¥∞∏°ø£®1£©![]() £®2£©
£®2£©![]() £®3£©¢Ÿ
£®3£©¢Ÿ![]() =
= ![]() ¢⁄
¢⁄![]()
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫£®1£©π˝µ„G◊ˆGH°ÕBD£¨¥π◊„Œ™H£¨GM°ÕFB£¨¥π◊„Œ™M£¨µ„E°¢FÕ¨ ±¥”µ„C≥ˆ∑¢£¨À˘“‘EC=CF=FM=GM=GH=![]() t£¨«“DG“≤ «°˜BDFµƒΩ«∆Ω∑÷œþ£¨”…°˜BDF°◊°˜ABCµ√£∫
t£¨«“DG“≤ «°˜BDFµƒΩ«∆Ω∑÷œþ£¨”…°˜BDF°◊°˜ABCµ√£∫ ![]() £¨°ýBD£Ω5
£¨°ýBD£Ω5![]() t£¨DF£Ω3
t£¨DF£Ω3![]() t£¨ø…«Ûµ√DL°¢BMµƒ≥§∂»£¨”…DL=DH£¨BH=BM£¨ππ‘Ïπÿ”⁄tµƒ∑Ω≥Ãø…“‘«Ûµ√¥∞∏£Æ
t£¨ø…«Ûµ√DL°¢BMµƒ≥§∂»£¨”…DL=DH£¨BH=BM£¨ππ‘Ïπÿ”⁄tµƒ∑Ω≥Ãø…“‘«Ûµ√¥∞∏£Æ
£®2£©µ„G‘⁄AB±þ…œ ±£¨π˝µ„G◊˜GH°ÕBC£¨¥π◊„Œ™H£¨”…£®1£©÷–µƒ ˝÷µ£¨Ω·∫œ°˜BGH°◊°˜BAC£¨ππ‘Ï≥ˆπÿ”⁄tµƒ∑Ω≥ã¨ø…“‘µ√µΩ¥∞∏£Æ
£®3£©£©”…DF°ŒACµ√µΩ°˜ABC°◊°˜DBF£¨°ý ![]() £¨º¥
£¨º¥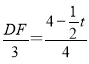 £¨µ√µΩDF£Ω
£¨µ√µΩDF£Ω![]() (8t)£¨∑÷¡Ω÷÷«ÈøˆÃ÷¬€£∫
(8t)£¨∑÷¡Ω÷÷«ÈøˆÃ÷¬€£∫
¢Ÿµ±0£ºt°Ð![]() ±£¨S£ΩS°˜DFG£ΩS°˜DEF=
±£¨S£ΩS°˜DFG£ΩS°˜DEF=![]() DFCF£Ω
DFCF£Ω![]() °¡
°¡![]() (8t)°¡
(8t)°¡![]() t=
t=![]() t2+
t2+![]() t£ª
t£ª
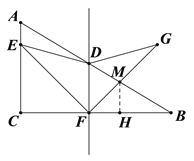
¢⁄µ±![]() £ºt°Ð6 ±£¨…ËGΩªAB”⁄µ„M£¨π˝µ„M◊˜MH°ÕBC”⁄H£¨…ËFH=MH=a£¨«Ûµ√BH£¨Ω‚≥ˆa”Îtµƒπÿœµ£¨ºÃ∂¯«Ûµ√S”Îtµƒπÿœµ£Æ
£ºt°Ð6 ±£¨…ËGΩªAB”⁄µ„M£¨π˝µ„M◊˜MH°ÕBC”⁄H£¨…ËFH=MH=a£¨«Ûµ√BH£¨Ω‚≥ˆa”Îtµƒπÿœµ£¨ºÃ∂¯«Ûµ√S”Îtµƒπÿœµ£Æ
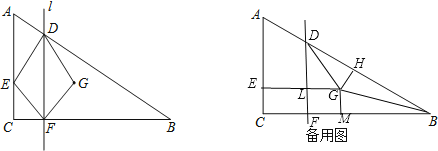
‘Ã‚Ω‚Œˆ£∫£®1£©![]()
…ËDF£¨EGœýΩª”⁄L£¨π˝µ„G◊ˆGH°ÕBD£¨¥π◊„Œ™H£¨GM°ÕFB£¨¥π◊„Œ™M£¨µ„E°¢FÕ¨ ±¥”µ„C≥ˆ∑¢£¨À˘“‘Àƒ±þ–ŒECFL°¢Àƒ±þ–ŒLFGM∂º «’˝∑Ω–Œ£¨
°ýEC=CF=FM=GM=GH=![]() t£¨
t£¨
”÷°þDG“≤ «°˜BDFµƒΩ«∆Ω∑÷œþ£¨
°ýDL=DH£¨
°þDF°ŒAC£¨
°ý°˜BDF°◊°˜BAC£¨
°ý![]() £¨
£¨
°ýBD£Ω5![]() t£¨DF£Ω3
t£¨DF£Ω3![]() t£¨
t£¨
”÷°þDL=DH=3![]() t
t![]() t£Ω3
t£Ω3![]() t£¨
t£¨
BH=BM=4-t£¨”÷°þBD=BH+HD£¨
°ý5![]() t£Ω3
t£Ω3![]() t+4t£¨Ω‚µ√£∫t=
t+4t£¨Ω‚µ√£∫t=![]() £Æ
£Æ
£®2£©![]()
µ„G‘⁄AB±þ…œ ±£¨π˝µ„G◊˜GH°ÕBC£¨¥π◊„Œ™H£¨
°þGH°ŒAC£¨
À˘“‘°˜BGH°◊°˜BAC£¨
°ý![]() £¨º¥£∫
£¨º¥£∫ 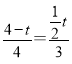 £¨
£¨
Ω‚µ√£∫t=![]() £Æ
£Æ
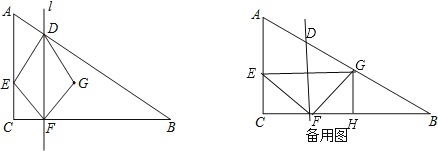
£®3£©°þDF°ŒAC
°ý°˜ABC°◊°˜DBF£¨
°ý![]() £¨
£¨
º¥ £¨Ω‚µ√
£¨Ω‚µ√![]()
¢Ÿµ±![]() ±£¨
±£¨
![]() =
= ![]()
¢⁄µ±![]() ±£¨…ËFGΩªAB”⁄µ„M£¨π˝µ„M◊˜MH°ÕBC”⁄H£¨…ËFH=MH=a£¨
±£¨…ËFGΩªAB”⁄µ„M£¨π˝µ„M◊˜MH°ÕBC”⁄H£¨…ËFH=MH=a£¨
‘ÚBH= ![]() £¨
£¨
°ý![]() £¨
£¨
Ω‚µ√![]()
![]()



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄°˜ABC÷–£¨°œACB=90°„£¨D «BCµƒ÷–µ„£¨DE°ÕBC£¨CE°ŒAD£¨»ÙAC=2£¨CE=4£¨‘ÚÀƒ±þ–ŒACEBµƒ÷Ð≥§Œ™ £Æ 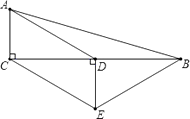
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø°∞–°Õ∑∞÷∞÷°±Œ™¡ÀºÏ≤È°∞¥ÛÕ∑∂˘◊”°±∂‘∆Ω––œþµƒÃıº˛”Ζ‘÷ ’‚≤ø∑÷÷™ ∂µƒ’∆Œ’«Èøˆ£¨∏¯À˚≥ˆ¡À“ªµ¿Ã‚£∫»ÁÕº£¨AB°ŒDE£¨°œB=80°„£¨CM∆Ω∑÷°œBCD£¨CN°ÕCM£¨«Û°œNCEµƒ∂» ˝£Æ°∞¥ÛÕ∑∂˘◊”°±…‘º”ÀºÀ˜£¨æÕ◊ˆ≥ˆ¿¥¡À£¨ƒ„÷™µ¿À˚ «‘ı—˘Ω‚µƒ¬£ø«Î∞—ƒ„µƒÕ∆¿Ìπ˝≥Ö¥œ¬¿¥∞…£Æ 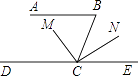
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™x3£´y3£Ω(x£´y)(x2£≠xy£´y2)≥∆Œ™¡¢∑Ω∫Õπ´ Ω£¨x3£≠y3£Ω(x£≠y)(x2£´xy£´y2)≥∆Œ™¡¢∑Ω≤Óπ´ Ω£¨æð¥À£¨ ‘Ω´œ¬¡–∏˜ Ω∑÷Ω‚“Ú Ω£∫
(1)a3£´8£ª°°°°°°°°°°°°°°(2)27a3£≠1.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øΩ‚œ¬¡–∑Ω≥ã∫
£®1£©£®x©Å5£©2=8£®x©Å5£©
£®2£©2x2©Å4x©Å3=0£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥–£ø™’π¡À°∞Œ“∂¡ È£¨Œ“øÏ¿÷°±Œ™÷˜Ã‚µƒµ˜≤ȪÓ∂Ø£¨∆‰÷–∆þƒÍº∂∂˛∞ý»´ÃÂÕ¨—ß“ª∏ˆ—ß∆⁄∆Ωæ˘“ªÃÏ‘ƒ∂¡øŒÕ‚ ȺÆÀ˘”√ ±º‰µƒ«Èøˆ»Áœ¬±Ì£∫
±º‰£®–° ±£© | 0.5 | 1 | 1.5 | 2 | 5 |
»À ˝£®√˚£© | 7»À | 18»À | 12»À | 3»À |
”…”⁄Ãӱ̵ƒÕ¨—ß≤ª–°–ƒ∞—ƒ´ÀƵŒ‘⁄¡À±Ì…œ£¨÷¬ π±Ì÷– ˝æð≤ªÕÍ’˚£¨µ´÷™µ¿À˘”√ ±º‰Œ™1–° ±µƒ»À ˝Œ™»´∞ý»À ˝µƒ36%£ÆΩ·∫œ…œ±Ìªÿ¥œ¬¡–Œ £∫
£®1£©∆þƒÍº∂∂˛∞ýπ≤”–∂ý…Ÿ»À£ø
£®2£©—ß…˙À˘”√ ±º‰µƒ÷⁄ ˝∫Õ÷–Œª ˝∑÷±Œ™∂ý…Ÿ–° ±£ø
£®3£©»Áπ˚∞—∏√∞ýµƒ—ß…˙µƒÀ˘”√ ±º‰«ÈøˆªÊ≥……»–ŒÕ≥º∆Õº£¨‘ÚÀ˘”√ ±º‰Œ™2–° ±µƒ»À ˝À˘∂‘”¶µƒ…»–Œ‘≤–ƒΩ«Œ™∂ý…Ÿ∂»£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄÷±Ω«»˝Ω«–Œ÷–£¨∆‰÷–“ª∏ˆ»ÒΩ« «¡Ì“ª∏ˆ»ÒΩ«µƒ2±∂£¨‘Ú¥À»˝Ω«–Œ÷–◊Ó–°µƒΩ« «£®°°°°£©
A. 15°„ B. 30°„ C. 60°„ D. 90°„
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø”–»ÁÕºÀ˘ 浃º◊°¢““°¢±˚≥§∑Ω–Œø®∆¨»Ù∏…’≈£¨”√À¸√«ø…“‘∆¥“ª–©–¬µƒ≥§∑Ω–Œ£Æ«Û≥§Œ™£®a+2b£©£¨øÌŒ™£®2a+b£©µƒ≥§∑Ω–Œ√ʪ˝£ª»Ù“™∆¥’‚—˘“ª∏ˆ≥§∑Ω–Œ£¨‘Ú–Ë“™º◊°¢““°¢±˚≥§∑Ω–Œø®∆¨∑÷±∂ý…Ÿ’≈£ø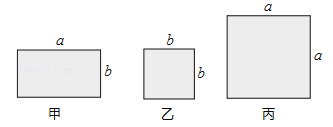
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∞—œ¬¡–∂ýœÓ Ω∑÷Ω‚“Ú Ω£∫
£®1£©4x2y2©Å4
£®2£©2pm2©Å12pm+18p£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com