
分析 (1)根据先把异分母转化成同分母,然后进行加减运算;
(2)根据解不等式,可得每个不等式的解集解集,根据不等式解集的公共部分是不等式组的解集,可得答案.
解答 解(1)原式=$\frac{{a}^{2}}{a-1}$-$\frac{(a+1)(a-1)}{a-1}$=$\frac{{a}^{2}-{a}^{2}+1}{a-1}$=$\frac{1}{a-1}$;
(2)由2x+3>x,解得x>-3,
由$\frac{1}{2}$x≥x-3,解得x≤6,
不等式组的解集为-3<x≤6.
点评 本题考查了分式的加减,分式的加减运算中,如果是同分母分式,那么分母不变,把分子直接相加减即可;如果是异分母分式,则必须先通分,把异分母分式化为同分母分式,然后再相加减.


科目:初中数学 来源: 题型:解答题
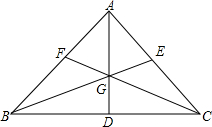 如图在△ABC中,点D、E、F分别在三边上,E是AC中点.AD、BE、CF交于点G,BD=2DC,S△GCE=4,S△GCD=5,求△ABC的面积?
如图在△ABC中,点D、E、F分别在三边上,E是AC中点.AD、BE、CF交于点G,BD=2DC,S△GCE=4,S△GCD=5,求△ABC的面积?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 42 | B. | 44 | C. | 48 | D. | 46 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com