
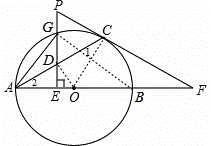
如图,已知AB,AC分别是⊙O的直径和弦,点G为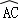 上一点,GE⊥AB,垂足为点E,交AC于点D,过点C的切线与AB的延长线交于点F,与EG的延长线交于点P,连接AG.
上一点,GE⊥AB,垂足为点E,交AC于点D,过点C的切线与AB的延长线交于点F,与EG的延长线交于点P,连接AG.
(1)求证:△PCD是等腰三角形;
(2)若点D为AC的中点,且∠F=30°,BF=2,求△PCD 的周长和AG的长.
的周长和AG的长.
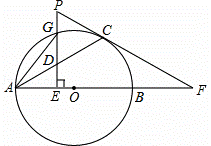
(1)证明:连结OC,如图,
∵PC为⊙O的切线,
∴OC⊥PC,
∴∠OCP=90°,即∠1+∠PCD=90°,
∵GE⊥AB,
∴∠GEA=90°,
∴∠2+∠ADE=90°,
∵OA=OC,
∴∠1=∠2,
∴∠PCD=∠ADE,
而∠ADE=∠PDC,
∴∠PCD=∠PDC,
∴△PCD是等腰三角形;
(2)解:连结OD,BG,如图,
在Rt△COF中,∠F=30°,BF=2,
∴OF=2OC,即OB+2=2OC,
而OB=OC,
∴OC=2,
∵∠FOC=90°﹣∠F=60°,
∴∠1=∠2=30°,
∴∠PCD=90°﹣∠1=60°,
∴△PCD为等边三 角形,
角形,
∵D为AC的中点,
∴OD⊥AC,
∴AD=CD,
在Rt△OCD中,OD=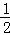 OC=1,
OC=1,
CD=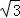 OD=
OD= ,
,
∴△PCD的周长为3 ;
;
在Rt△ADE中,AD=CD= ,
,
∴DE=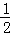 AD=
AD=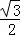 ,
,
AE=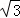 DE=
DE=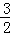 ,
,
∵AB为直径,
∴∠AGB=90°,
而∠GAE=∠BAG,
∴Rt△AGE∽Rt△ABG,
∴AG:AB =AE:AG,
=AE:AG,
∴AG2=AE•AB=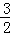 ×4=6,
×4=6,
∴AG=6.


科目:初中数学 来源: 题型:
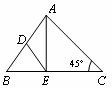
如图,四边形ABCD、AEFG是正方形,点E、G分别在AB,AD上,连接FC,过点E作EH//FC,交BC于点H.若AB=4,AE=1,则BH的长为
(A)1. (B)2. (C)3. (D)3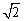 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
关于x的一元二次方程x2+2(m﹣1)x+m2=0的两个实数根分别为x1,x2,且x1+x2>0,x1x2>0,则m的取值范围是( )
|
| A. | m≤ | B. | m≤ | C. | m<1 | D. | m<1且m≠0 |
查看答案和解析>>
科目:初中数学 来源: 题型:
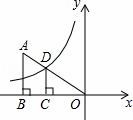
如图,在平面直角坐标系中,Rt△ABO的顶点O与原点重合,顶点B在x轴上,∠ABO=90°,OA与反比例函数y=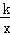 的图象交于点D,且OD=2AD,过点D作x轴的垂线交x轴于点C.若S四边形ABCD=10,则k的值为 .
的图象交于点D,且OD=2AD,过点D作x轴的垂线交x轴于点C.若S四边形ABCD=10,则k的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
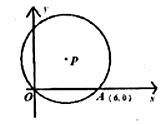
如图,在平面直角坐标系中,点O为坐标原点,点P在第一象限,⊙P与x轴交于O,A两点,点A的坐标为(6,0),⊙P的半径为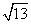 ,则点P的坐标为__________。
,则点P的坐标为__________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com