
【题目】如图,在平面直角坐标系中,将点![]() 绕原点
绕原点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 得到点
得到点![]() ,则点
,则点![]() 的坐标为( )
的坐标为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
过点P作PA⊥x轴于点A,作P'B⊥x轴于点B,根据点P的坐标求出PA、OA的长度,根据旋转的性质得出P'O=OP,证明△P'OB≌△OPA,即可得解.
如图,过点P作PA⊥x轴于点A,作P'B⊥x轴于点B.
∵点P(3,4),∴PA=4,OA=3.
∵点P(3,4)绕坐标原点逆时针旋转90°得到点P',
∴P'O=PO,P'O⊥PO,
∴∠P'OP=90°,
∴∠P'OB+∠POA=90°.
∵∠POA+∠OPA=90°,
∴∠P'OB=∠OPA.
∵∠P'OB=∠OPA,∠P'BO=∠OAP=90°,P'O=OP,
∴△P'OB≌△OPA,∴OB=PA=4,P'B=OA=3,
∴点P'的坐标是(﹣4,3).
故选C.



科目:初中数学 来源: 题型:
【题目】如图所示是一块含30°,60°,90°的直角三角板,直角顶点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数y1=![]() (x>0)的图象上,顶点B在函数y2=
(x>0)的图象上,顶点B在函数y2= ![]() (x>0)的图象上,∠ABO=30°,则
(x>0)的图象上,∠ABO=30°,则![]() =( )
=( )
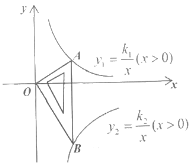
A.-3 B.3 C.![]() D.-
D.- ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,如图是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③方程ax2+bx+c=0的两根分别为﹣3和1;④b2﹣4ac>0,其中正确的命题有( )
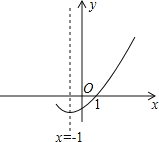
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 为倡导“低碳生活”,常选择以自行车作为代步工具,如图1所示是一辆自行车的实物图.车架档AC与CD的长分别为45cm,60cm,且它们互相垂直,座杆CE的长为20cm,点A,C,E在同一条直线上,且∠CAB=75°,如图2.
(1)求车架档AD的长;
(2)求车座点E到车架档AB的距离.
(结果精确到1 cm.参考数据: sin75°="0.966," cos75°=0.259,tan75°=3.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天能售出20件,每件盈利40元。经调查发现:如果这种衬衫的售价每降低1元时,平均每天能多售出2件.设每件衬衫降价x元.
(1)降价后,每件衬衫的利润为_____元,销量为_____件;(用含x的式子表示)
(2)为了扩大销售,尽快减少库存,商场决定釆取降价措施。但需要平均每天盈利1200元,求每件衬衫应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=mx2﹣(2m+1)x+m﹣5的图象与x轴有两个公共点.
(1)求m的取值范围;
(2)若m取满足条件的最小的整数,当n≤x≤1时,函数值y的取值范围是﹣6≤y≤24,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线![]() 交AB,BC分别于点M,N,反比例函数
交AB,BC分别于点M,N,反比例函数![]() 的图象经过点M,N.
的图象经过点M,N.
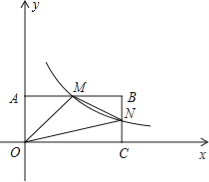
(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com