
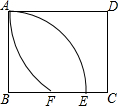
 如图,矩形ABCD中,AB=12,BC=13,以B为圆心,BA为半径画弧,交BC于点E,以D为圆心,DA为半径画弧,交BC于点F,则EF的长为( )
如图,矩形ABCD中,AB=12,BC=13,以B为圆心,BA为半径画弧,交BC于点E,以D为圆心,DA为半径画弧,交BC于点F,则EF的长为( )| A. | 3 | B. | 4 | C. | $\frac{9}{2}$ | D. | 5 |
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:填空题
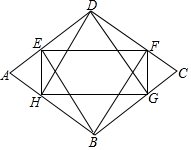 如图,在菱形ABCD中,分别过B、D作对边的垂线,垂足分别为E、F、G、H.若四边形EFGH的面积与菱形ABCD的面积之比为4:9,则sinA=$\frac{2\sqrt{2}}{3}$或$\frac{\sqrt{5}}{3}$.
如图,在菱形ABCD中,分别过B、D作对边的垂线,垂足分别为E、F、G、H.若四边形EFGH的面积与菱形ABCD的面积之比为4:9,则sinA=$\frac{2\sqrt{2}}{3}$或$\frac{\sqrt{5}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
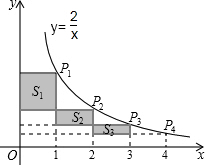 如图,在反比例函数y=$\frac{2}{x}$(x>0)的图象上,有点P1,P2,P3,P4,它们的横坐标依次为1,2,3,4,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,则S1+S2+S3=( )
如图,在反比例函数y=$\frac{2}{x}$(x>0)的图象上,有点P1,P2,P3,P4,它们的横坐标依次为1,2,3,4,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,则S1+S2+S3=( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 数量/本 | 15 | 11 | 8 | 4 | 3 | 2 |
| 人数 | 8 | 6 | 5 | 10 | 4 | 7 |
| A. | 该学校中参与调查的青年教师人数为40人 | |
| B. | 该学校中青年教师2016年平均每人阅读8本书 | |
| C. | 该学校中青年教师2016年度看书数量的中位数为4本 | |
| D. | 该学校中青年教师2016年度看书数量的众数为4本 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在哈市地铁2号线的建设中,甲、乙两个建设公司同时挖掘两段长度相等的隧道,如图是甲、乙两公司挖掘隧道长度y(米)与挖掘时间x(时)之间关系的部分图象.如果甲队施工速度始终不变,乙队在开挖6小时后,施工速度每小时增加了7米,结果两队同时完成了任务,那么甲队从开挖到完工所挖隧道的总长度为( )米.
在哈市地铁2号线的建设中,甲、乙两个建设公司同时挖掘两段长度相等的隧道,如图是甲、乙两公司挖掘隧道长度y(米)与挖掘时间x(时)之间关系的部分图象.如果甲队施工速度始终不变,乙队在开挖6小时后,施工速度每小时增加了7米,结果两队同时完成了任务,那么甲队从开挖到完工所挖隧道的总长度为( )米.| A. | 100 | B. | 110 | C. | 120 | D. | 130 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
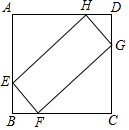 如图,正方形ABCD,AB=8,点E,F,G,H分别在正方形ABCD的边上(不与正方形的顶点重合),设BF=m,EF:FG=1:k,其中k≥1,若四边形EFGH是矩形,
如图,正方形ABCD,AB=8,点E,F,G,H分别在正方形ABCD的边上(不与正方形的顶点重合),设BF=m,EF:FG=1:k,其中k≥1,若四边形EFGH是矩形,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
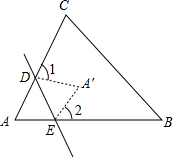 如图所示,一张△ABC纸片,点D,E分别在线段AC,AB上,将△ADE沿着DE折叠,A与A′重合,若∠A=α,则∠1+∠2=( )
如图所示,一张△ABC纸片,点D,E分别在线段AC,AB上,将△ADE沿着DE折叠,A与A′重合,若∠A=α,则∠1+∠2=( )| A. | α | B. | 2α | C. | 180°-α | D. | 180°-2α |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com