
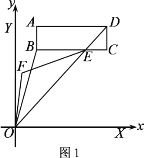
【题目】如图,长方形ABCD在平面直角坐标系中,点A(1,8),B(1,6),C(7,6),点X,Y分别在x,y轴上.
(1)请直接写出D点的坐标 ;
(2)连接OB、OD,OD交BC于点E,∠BOY的平分线和∠BEO的平分线交于点F,若∠BOE=n,求∠OFE的度数.
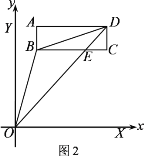
(3)若长方形ABCD以每秒![]() 个单位的速度向下运动,设运动时间为t秒,问在第一象限内是否存在某一时刻t,使△OBD的面积等于长方形ABCD的面积的
个单位的速度向下运动,设运动时间为t秒,问在第一象限内是否存在某一时刻t,使△OBD的面积等于长方形ABCD的面积的![]() ?若存在,请求出t的值,若不存在,请说明理由。
?若存在,请求出t的值,若不存在,请说明理由。
【答案】(1)(7,8);(2)∠EFO=135°-![]() n;(3)存在,t=2.
n;(3)存在,t=2.
【解析】
(1)由长方形的性质得出AB=DC,AD=BC,由题意得出AB=DC=2,即可得出D点的坐标;
(2)设∠BEO=2x,则∠EOX=2x,作FG∥OX,得出![]() ,由角平分线得出
,由角平分线得出![]() ,得出
,得出![]() ,由平行线得出∠EFG=∠BEF=x,得出
,由平行线得出∠EFG=∠BEF=x,得出![]() ,即可得出∠OFE的度数;
,即可得出∠OFE的度数;
(3)作AM⊥y轴于M,先求出矩形ABCD的面积,△OBD的面积=△ODM的面积-△ABD的面积-梯形AMOB的面积,得出方程,解方程即可求出t的值.
解:(1)∵四边形ABCD是长方形,
∴AB=DC,AD=BC,
∵点A(1,8),B(1,6),C(7,6),
∴AB=DC=2,
∴D点的坐标为:(7,8);
故答案为:(7,8);
(2)∵∠BOY的平分线和∠BEO的平分线交于点F,
![]()
∵BC∥OX,
∴∠BEO=∠EOX,
设∠BEO=2x,
则∠EOX=2x,
作FG∥OX,如图1所示:
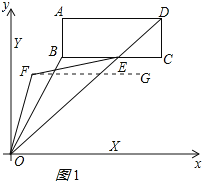
则![]()
又![]()
![]()
∵BC∥FG∥OX,
∴∠EFG=∠BEF=x,
![]()
![]()
(3)存在某一时刻,使△OBD的面积等于长方形ABCD面积的![]() ,t=2;理由如下:
,t=2;理由如下:
作AM⊥y轴于M,如图2所示:
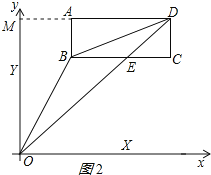
∵S矩形ABCD=2×6=12,
S△OBD=S△ODM-S△ABD-S梯形AMOB= ![]()
![]()
解得:t=2.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】请认真观察图形,解答下列问题:
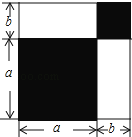
(1)根据图中条件,用两种方法表示两个阴影图形的面积的和(只需表示,不必化简);
(2)由(1),你能得到怎样的等量关系?请用等式表示;
(3)如果图中的a,b(a>b)满足a2+b2=53,ab=14,求:①a+b的值;②a4﹣b4的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(﹣1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
(1)求抛物线的解析式;
(2)求△MCB的面积S△MCB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为一台灯示意图,其中灯头连接杆DE始终和桌面FG平行,灯脚AB始终和桌面FG垂直,

(1)当∠EDC=∠DCB=120°时,求∠CBA;
(2)连杆BC、CD可以绕着B、C和D进行旋转,灯头E始终在D左侧,设∠EDC,∠DCB,∠CBA的度数分别为α,β,γ,请画出示意图,并直接写出示意图中α,β,γ之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBEF是菱形?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校课外小组为了解同学们对学校“阳光跑操”活动的喜欢程度,抽取部分学生进行调查,被调查的每个学生按![]() (非常喜欢)、
(非常喜欢)、![]() (比较喜欢)、
(比较喜欢)、![]() (一般)、D(不喜欢)四个等级对活动进行评价,图①和图②是该小组采集数据后绘制的两幅不完整的统计图. 请根据统计图提供的信息,解答下列问题:
(一般)、D(不喜欢)四个等级对活动进行评价,图①和图②是该小组采集数据后绘制的两幅不完整的统计图. 请根据统计图提供的信息,解答下列问题:

(1)求参与此次调査的学生人数;
(2)补画出图②中不完整的部分;
(3)如果该校有6000名学生,请估计对“阳光跑操”活动“非常喜欢”的学生有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=ax+b的图象上有两点A、B,它们的横坐标分别是3,-1,若二次函数y=![]() x2的图象经过A、B两点.
x2的图象经过A、B两点.
(1)请求出一次函数的表达式;
(2)设二次函数的顶点为C,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,正方形![]() 中,点E在
中,点E在![]() 上,点F在
上,点F在![]() 上,连接
上,连接![]() 、
、![]() 、
、![]() .且
.且![]() 平分
平分![]() .
.

(1)如图1,求证:![]() .
.
(2)如图2,若点E为BC的中点,![]() ,求
,求![]() 的面积.
的面积.
(3)如图3,若∠B=90°,连接BD分别交AF、AE于M、N两点,连接ME,若ME⊥AF于M, BM:EF=4![]() :5,△AEF的面积为15时,求AE的长度.
:5,△AEF的面积为15时,求AE的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com