
【题目】已知,直线AB∥DC,点P为平面上一点,连接AP与CP.
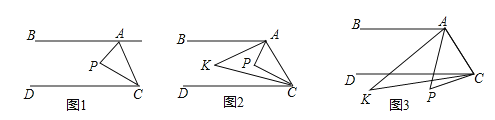
(1)如图1,点P在直线AB、CD之间,当∠BAP=60°,∠DCP=20°时,则∠APC= .
(2)如图2,点P在直线AB、CD之间,∠BAP与∠DCP的角平分线相交于点K,写出∠AKC与∠APC之间的数量关系为 .
(3)如图3,点P落在CD外,∠BAP与∠DCP的角平分线相交于点K,∠AKC与∠APC有何数量关系?并说明理由.
【答案】(1)80°;(2)∠AKC=![]() ∠APC;(3)∠AKC=
∠APC;(3)∠AKC=![]() ∠APC.
∠APC.
【解析】试题分析:(1)过P作PE∥AB,根据平行线的性质即可得到∠APE=∠BAP,∠CPE=∠DCP,再根据![]() 进行计算即可;
进行计算即可;
(2)过K作KE∥AB,根据KE∥AB∥CD,可得∠AKE=∠BAK,∠CKE=∠DCK,得到∠AKC=∠AKE+∠CKE=∠BAK+∠DCK,同理可得,∠APC=∠BAP+∠DCP,再根据角平分线的定义,得![]() 进而得到
进而得到![]()
(3)过K作KE∥AB,根据KE∥AB∥CD,可得∠BAK=∠AKE,∠DCK=∠CKE,进而得到∠AKC=∠AKE∠CKE=∠BAK∠DCK,同理可得,∠APC=∠BAP∠DCP,再根据角平分线的定义,得出![]() 进而得到
进而得到![]()
试题解析:(1)如图1,过P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠APE=∠BAP,∠CPE=∠DCP,
∴![]()
(2) ![]()

理由:如图2,过K作KE∥AB,
∵AB∥CD,
∴KE∥AB∥CD,
∴∠AKE=∠BAK,∠CKE=∠DCK,
∴∠AKC=∠AKE+∠CKE=∠BAK+∠DCK,
过P作PF∥AB,
同理可得,∠APC=∠BAP+∠DCP,
∵∠BAP与∠DCP的角平分线相交于点K,
∴![]()
∴![]()
(3) ![]()
理由:如图3,过K作KE∥AB,
∵AB∥CD,
∴KE∥AB∥CD,
∴∠BAK=∠AKE,∠DCK
∴∠AKC=∠AKE∠CKE=∠BAK∠DCK,
过P作PF∥AB,
同理可得,∠APC=∠BAP∠DCP,
∵∠BAP与∠DCP的角平分线相交于点K,
∴![]()
∴![]()


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点分别为A(2,3)、B(3,1)、C(﹣2,﹣2).

(1)请在图中作出△ABC关于直线x=﹣1的轴对称图形△DEF(A、B、C的对应点分别是D、E、F),并直接写出D、E、F的坐标;
(2)求四边形ABED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“春种一粒栗,秋收万颗子”,唐代诗人李绅这句诗中的“粟”即谷子(去皮后则称为“小米”),被誉为中华民族的哺育作物。我省有着“小杂粮王国”的美誉,谷子作为我省杂粮谷物中的大类,其种植面积已连续多年全国第一.2016年全国谷子的种植面积为2000万亩,年总产量为150万吨,我省谷子平均亩产量为160kg,国内其他地区谷子的平均亩产量为60kg.请解答下列问题:
(1)求我省2016年谷子的种植面积是多少万亩;
(2)2017年,若我省谷子的平均亩产量仍保持160kg不变,要使我省谷子的年总产量达到52万吨,那么今年我省应再多种植多少万亩的谷子?
查看答案和解析>>
科目:初中数学 来源: 题型:
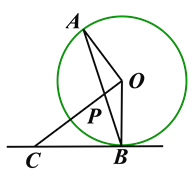
【题目】如图,AB是⊙O的弦,点C是在过点B的切线上,且OC⊥OA,OC交AB于点P.
(1)判断△CBP的形状,并说明理由;
(2)若⊙O的半径为6,AP=![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】资料:小球沿直线撞击水平格档反弹时(不考虑垂直撞击),撞击路线与水平格档所成的锐角等于反弹路线与水平格档所成的锐角.以图(1)为例,如果黑球 ![]() 沿从
沿从 ![]() 到
到 ![]() 方向在
方向在 ![]() 点处撞击
点处撞击 ![]() 边后将沿从
边后将沿从 ![]() 到
到 ![]() 方向反弹,根据反弹原则可知
方向反弹,根据反弹原则可知 ![]() ,即
,即 ![]() .如图(2)和(3),
.如图(2)和(3),![]() 是一个长方形的弹子球台面,有黑白两球
是一个长方形的弹子球台面,有黑白两球 ![]() 和
和 ![]() ,小球沿直线撞击各边反弹时遵循资料中的反弹原则.(回答以下问题时将黑白两球均看作几何图形中的点,不考虑其半径大小)
,小球沿直线撞击各边反弹时遵循资料中的反弹原则.(回答以下问题时将黑白两球均看作几何图形中的点,不考虑其半径大小)

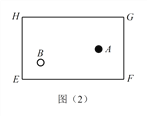
(1)探究(1):黑球 ![]() 沿直线撞击台边
沿直线撞击台边 ![]() 哪一点时,可以使黑球
哪一点时,可以使黑球 ![]() 经台边
经台边 ![]() 反弹一次后撞击到白球
反弹一次后撞击到白球 ![]() ?请在图(2)中画出黑球
?请在图(2)中画出黑球 ![]() 的路线图,标出撞击点,并简单证明所作路线是否符合反弹原则.
的路线图,标出撞击点,并简单证明所作路线是否符合反弹原则.
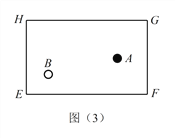
(2)探究(2):黑球 ![]() 沿直线撞击台边
沿直线撞击台边 ![]() 哪一点时,可以使黑球
哪一点时,可以使黑球 ![]() 先撞击台边
先撞击台边 ![]() 反弹一次后,再撞击台边
反弹一次后,再撞击台边 ![]() 反弹一次撞击到白球
反弹一次撞击到白球 ![]() ?请在图(3)中画出黑球
?请在图(3)中画出黑球 ![]() 的路线图,标出黑球撞击
的路线图,标出黑球撞击 ![]() 边的撞击点,简单说明作法,不用证明.
边的撞击点,简单说明作法,不用证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)
【感受联系】在初二的数学学习中,我们感受过等腰三角形与直角三角形的密切联系.等腰三角形作底边上的高线可转化为直角三角形,直角三角形沿直角边翻折可得到等腰三角形等等.
【探究发现】某同学运用这一联系,发现了“30°角所对的直角边等于斜边的一半”.并给出了如下的部分探究过程,请你补充完整证明过程
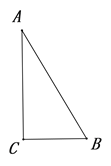
已知:如图,在![]() △
△![]() 中,
中, ![]() °,
°,![]() °.
°.
求证: ![]() .
.
证明:
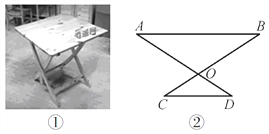
【灵活运用】该同学家有一张折叠方桌如图①所示,方桌的主视图如图②.经测得![]() ,
, ![]() ,将桌子放平,两条桌腿叉开的角度
,将桌子放平,两条桌腿叉开的角度![]() .
.
求:桌面与地面的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
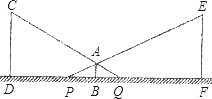
【题目】小明利用灯光下自己的影子长度来测量路灯的高度.如图,CD和EF是两等高的路灯,相距27m,身高1.5m的小明(AB)站在两路灯之间(D、B、F共线),被两路灯同时照射留在地面的影长BQ=4m,BP=5m.
(1)小明距离路灯多远?
(2)求路灯高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
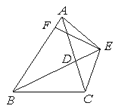
【题目】已知:如图,BD为△ABC的的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF.其中正确的是( )
A.①②③ B.①③④ C.①②④ D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蓄水池的排水管每小时排水8m3,6小时可将满池水全部排空.
(1)蓄水池的容积是____________ m3;
(2)如果增加排水管,使每小时排水量达到Q(m3),那么将满池水排空所需时间为t(小时),则Q与t之间关系式为____________;
(3)如果准备在5小时内将满池水排空,那么每小时的排水量至少为____________ m3/小时;
(4)已知排水管最多为每小时12m3,则至少____________小时可将满池水全部排空.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com