
【题目】如图,已知AB是⊙O的直径,BE是⊙O的弦,BC是∠ABE的平分线且交⊙O于点C,连接AC,CE,过点C作CD⊥BE,交BE的延长线于点D.
(1)∠DCE ∠CBE;(填“>”“<”或“=”)
(2)求证:DC是⊙O的切线;
(3)若⊙O的直径为10,sin∠BAC=![]() ,求BE的长.
,求BE的长.
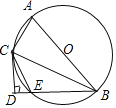
【答案】(1)=;(2)见解析;(3)2.8.
【解析】
(1)由AB为⊙O的直径,得到∠ACB=90°,求得∠ACB=∠D,根据角平分线的性质得到∠ABC=∠CBD,通过相似三角形得到∠BAC=∠BCD,四边形ABEC是圆内接四边形,得出∠CED=∠BAC,根据余角的性质即可证得∠DCE=∠CBE;
(2)连接OC,由等腰三角形的性质得出∠OBC=∠OCB,等量代换得到∠OCB=∠CBD,证得OC∥BD,即可证得OC⊥CD,即可得到结论;
(3)解直角三角形ABC求得BC,进而求得AC,通过三角形相似的性质得出CD=4.8,BD=6.4,进而求得DE=3.6,即可求得BE=2.8.
(1)解:∵AB为⊙O的直径,
∴∠ACB=90°,
∵CD⊥BE
∠D=90°,
∴∠ACB=∠D,
∵BC是∠ABE的平分线,
∴∠ABC=∠CBD,
∴△ABC∽△CBD,
∴∠BAC=∠BCD,
∵四边形ABEC是圆内接四边形
∴∠CED=∠BAC,
∵∠DBC+∠BCD=90°,∠ECD+∠CED=90°
∴∠DCE=∠CBE;
故答案为:=;
(2)证明:连接OC,
∵OB=OC,
∴∠OBC=∠OCB,
∵∠ABC=∠CBD
∴∠OCB=∠CBD,
∴OC∥BD,
∵CD⊥BD,
∴OC⊥CD,
∴CD是⊙O的切线;
(3)解:∵⊙O的直径为10,sin∠BAC=![]() ,
,
∴sin∠BAC=![]() =
=![]() ,
,
∴BC=8,
∴AC=![]() =6,
=6,
∵△ABC∽△CBD,
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,
,
∴CD=4.8,BD=6.4,
∵∠CDE=∠ACB=90°,∠CED=∠BAC,
∴△CED∽△BAC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴DE=3.6,
∴BE=BD﹣DE=6.4﹣3.6=2.8.


科目:初中数学 来源: 题型:
【题目】冬季来临,某网店准备在厂家购进![]() ,
,![]() 两种暖手宝共
两种暖手宝共![]() 个用于销售,若购买
个用于销售,若购买![]() 种暖手宝
种暖手宝![]() 个,
个,![]() 种暖手宝
种暖手宝![]() 个,需要
个,需要![]() 元;若购买
元;若购买![]() 种暖手宝
种暖手宝![]() 个,
个,![]() 种暖手宝
种暖手宝![]() 个,则需要
个,则需要![]() 元
元
(1)购买![]() ,
,![]() 两种暖手宝每个各需多少元?
两种暖手宝每个各需多少元?
(2)①由于资金限制,用于购买这两种暖手宝的资金不能超过![]() 元,设购买
元,设购买![]() 种暖手宝
种暖手宝![]() 个,求
个,求![]() 的取值范围;
的取值范围;
②在①的条件下,购进![]() 种暖手宝不能少于
种暖手宝不能少于![]() 个,则有哪几种购买方案?
个,则有哪几种购买方案?
(3)购买后,若一个![]() 种暖手宝运费为
种暖手宝运费为![]() 元,一个
元,一个![]() 种暖手宝运费为
种暖手宝运费为![]() 元,在第
元,在第![]() 问的各种购买方案中,购买
问的各种购买方案中,购买![]() 个暖手宝,哪一种购买方案所付的运费最少?最少运费是多少元?
个暖手宝,哪一种购买方案所付的运费最少?最少运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为实现2020年全面脱贫的目标,我国实施“精准扶贫”战略,从而使贫困户的生活条件得到改善,生活质量明显提高.为了切实关注、关爱贫困家庭学生,某校对全校各班贫困家庭学生的人数情况进行了统计,统计发现班上贫困家庭学生人数分别有2名,3名,4名,5名,6名,共五种情况.并将其制成了如下两幅不完整的统计图:
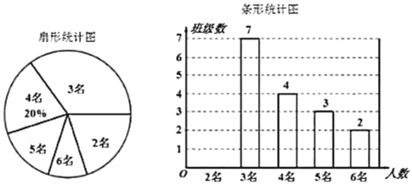
请回答下列问题:
(1)求该校一共有班级________个;在扇形统计图中,贫困家庭学生人数有5名的班级所对应扇形圆心角为________°;
(2)将条形图补充完整;
(3)甲、乙、丙是贫困生中的三名学生,学校决定从这三名学生中随机抽取两名代表到市里进行发言,用列表法或画树状图法,求同时抽到甲,乙两名学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数C:y=(x﹣2)2﹣2(0≤x≤3),点P在二次函数C的图象上,点A为x轴正半轴上一点,若tan∠AOP=1,则点P的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区山峰的高度每增加1百米,气温大约降低0.6℃.气温T(℃)和高度h(百米)的函数关系如图所示.请根据图象解决下列问题:
(1)求高度为5百米时的气温.
(2)求T关于h的函数表达式.
(3)测得山顶的气温为6℃,求该山峰的高度.
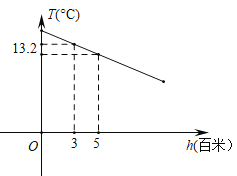
查看答案和解析>>
科目:初中数学 来源: 题型:
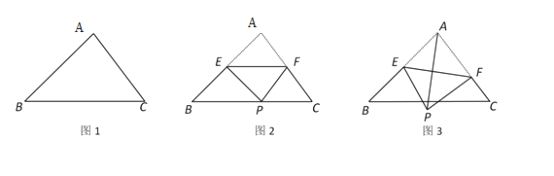
【题目】如图,在△ABC中,AB=![]() ,∠B=45°,∠C=60°.
,∠B=45°,∠C=60°.
(1)求BC边上的高线长.
(2)点E为线段AB的中点,点F在边AC上,连结EF,沿EF将△AEF折叠得到△PEF.
①如图2,当点P落在BC上时,求∠AEP的度数.
②如图3,连结AP,当PF⊥AC时,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=![]() AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BCCF=2HE.其中正确的结论有( )
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BCCF=2HE.其中正确的结论有( )
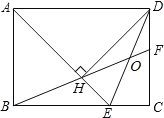
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
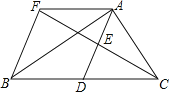
【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:D是BC的中点;
(2)若BA⊥AC,试判断四边形AFBD的形状,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com