
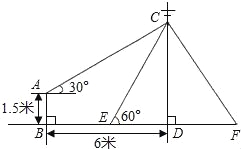
【题目】如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置高为1.5米的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长(结果保留小数点后一位,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73).
≈1.73).
【答案】拉线CE的长约为5.7米
【解析】
试题分析:由题意可先过点A作AH⊥CD于H.在Rt△ACH中,可求出CH,进而CD=CH+HD=CH+AB,再在Rt△CED中,求出CE的长.
试题解析:过点A作AH⊥CD,垂足为H,
由题意可知四边形ABDH为矩形,∠CAH=30°,
∴AB=DH=1.5,BD=AH=6,
在Rt△ACH中,tan∠CAH=![]() ,
,
∴CH=AHtan∠CAH,
∴CH=AHtan∠CAH=6tan30°=6×![]() (米),∵DH=1.5,∴CD=2
(米),∵DH=1.5,∴CD=2![]() +1.5,
+1.5,
在Rt△CDE中,∵∠CED=60°,sin∠CED=![]() ,
,
∴CE=![]() =4+
=4+![]() ≈5.7(米),
≈5.7(米),
答:拉线CE的长约为5.7米.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某长途汽车客运公司规定:旅客可随身携带一定质量的行李,若超过规定的质量,则需要购买行李票.已知行李费y(元)是关于x(kg)的一次函数,王先生带60 kg行李需付6元行李费,张先生带80 kg行李需付10元行李费.
(1)求y与x之间的函数表达式.
(2)问:旅客最多可免费携带多少千克行李?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】空气是由多种气体混合而成的,为了直观地介绍空气各成分的百分比,最适合使用的统计图是______(从“条形图,扇形图,折线图和直方图”中选一个)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]()
(2)(p﹣q)4÷(q﹣p)3(p﹣q)2
(3)aa2a3+(﹣2a3)2﹣a8÷a2
(4)(﹣2x)2(x2)3÷(﹣x)2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点.若AE=2,当EF+CF取得最小值时,∠ECF的度数为( )

A. 20° B. 25° C. 30° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城市平均每天产生垃圾700 t,由甲、乙两家垃圾处理厂处理.已知甲厂每小时可处理垃圾55 t,费用为550元;乙厂每小时可处理垃圾45 t,费用为495元.
(1)如果甲、乙两厂同时处理该城市的垃圾,那么每天需几小时?
(2)如果该城市规定每天用于处理垃圾的费用不得高于7370元,那么至少安排甲厂处理几小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线y=x2+3先向左平移2个单位,再向下平移1个单位,所得新抛物线的解析式为( )
A.y=(x+2)2+2B.y=(x﹣1)2+5C.y=(x+2)2+4D.y=(x﹣2)2+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标为(-2,3),点B的坐标为(-2,-3),那么点A和点B的位置关系是( )
A. 关于x轴对称 B. 关于y轴对称
C. 关于原点对称 D. 关于坐标轴和原点都不对称
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com