
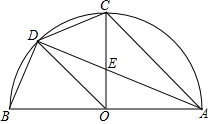
 如图,AB是半圆直径,半径OC⊥AB于点O,D为半圆上一点,AC∥OD,AD与OC交于点E,连结CD、BD,给出以下三个结论:①OD平分∠COB;②BD=CD;③CD2=CE•CO,其中正确结论的序号是①②③.
如图,AB是半圆直径,半径OC⊥AB于点O,D为半圆上一点,AC∥OD,AD与OC交于点E,连结CD、BD,给出以下三个结论:①OD平分∠COB;②BD=CD;③CD2=CE•CO,其中正确结论的序号是①②③. 分析 ①由OC⊥AB就可以得出∠BOC=∠AOC=90°,再由OC=OA就可以得出∠OCA=∠OAC=45°,由AC∥OD就可以得出∠BOD=45°,进而得出∠DOC=45°,从而得出结论;
②由∠BOD=∠COD即可得出BD=CD;
③由∠AOC=90°就可以得出∠CDA=45°,得出∠DOC=∠CDA,就可以得出△DOC∽△EDC.进而得出$\frac{DC}{EC}=\frac{OC}{DC}$,得出CD2=CE•CO.
解答 解:①∵OC⊥AB,
∴∠BOC=∠AOC=90°.
∵OC=OA,
∴∠OCA=∠OAC=45°.
∵AC∥OD,
∴∠BOD=∠CAO=45°,
∴∠DOC=45°,
∴∠BOD=∠DOC,
∴OD平分∠COB.故①正确;
②∵∠BOD=∠DOC,
∴BD=CD.故②正确;
③∵∠AOC=90°,
∴∠CDA=45°,
∴∠DOC=∠CDA.
∵∠OCD=∠OCD,
∴△DOC∽△EDC,
∴$\frac{DC}{EC}=\frac{OC}{DC}$,
∴CD2=CE•CO.故③正确.
故答案为:①②③.
点评 本题考查了圆周角定理,平行线的性质,圆的性质,圆心角与弦的关系定理的运用,相似三角形的判定及性质;熟练掌握圆周角定理和相似三角形的判定与性质是解决问题的关键.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:选择题
 如图,10个不同的正偶数按下图排列,箭头上方的每个数都等于其下方两数的和,如
如图,10个不同的正偶数按下图排列,箭头上方的每个数都等于其下方两数的和,如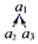 ,表示a1=a2+a3,则a1的最小值为( )
,表示a1=a2+a3,则a1的最小值为( )| A. | 32 | B. | 36 | C. | 38 | D. | 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
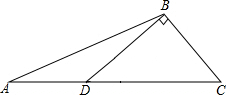 如图,在钝角△ABC中,过钝角顶点B作BD⊥BC交AC于点D.请用尺规作图法在BC边上求作一点P,使得点P到AC的距离等于BP的长.(保留作图痕迹,不写作法)
如图,在钝角△ABC中,过钝角顶点B作BD⊥BC交AC于点D.请用尺规作图法在BC边上求作一点P,使得点P到AC的距离等于BP的长.(保留作图痕迹,不写作法)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com