
 如图所示,圆A和圆B的半径都为1,AB=8.圆A和圆B都和圆O外切,且三圆均和直线l相切,切点为C、D、E,则圆O的半径为( )
如图所示,圆A和圆B的半径都为1,AB=8.圆A和圆B都和圆O外切,且三圆均和直线l相切,切点为C、D、E,则圆O的半径为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 如图,连接AC、BE、AB、AO、OB、OD,OD与AB交于点M.设⊙O半径为R,在RT△AOM中利用勾股定理即可解决.
解答 解:如图,连接AC、BE、AB、AO、OB、OD,OD与AB交于点M.设⊙O半径为R.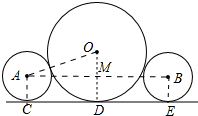
∵AC⊥CE,DO⊥CE,BE⊥CE,
∴AC∥OD∥BE,
∵AC=BE=1,
∴四边形ACEB是平行四边形,
∵∠ACD=∠ODC=∠BEC=90°,
∴四边形ACEB是矩形,
∴DM=AC=1,
∵AB∥CE,OD⊥CE,
∴OD⊥AB
∵OA=OB,
∴AM=BM=$\frac{1}{2}$AB=4,
在RT△AOM中,∵OA2=OM2+AM2,
∴(R+1)2=42+(R-1)2,
∴R=4
故选B.
点评 本题考查相切两个圆的性质、切线的性质、勾股定理等知识,解题的关键是设参数,构建方程解决问题,学会用方程的思想思考问题,属于中考常考题型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
 如图是某班50名同学爱心捐款额的频数分布直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最多的一组是( )
如图是某班50名同学爱心捐款额的频数分布直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最多的一组是( )| A. | 5-10元 | B. | 10-15元 | C. | 15-20元 | D. | 20-25元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9800名学生是总体 | B. | 每个学生是个体 | ||
| C. | 100名学生是所抽取的一个样本 | D. | 样本容量是100 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
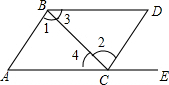 如图所示,点E在AC的延长线上,下列条件中不能判断AC∥BD的是( )
如图所示,点E在AC的延长线上,下列条件中不能判断AC∥BD的是( )| A. | ∠3=∠4 | B. | ∠D=∠DCE | C. | ∠1=∠2 | D. | ∠D+∠ACD=180° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com