
【题目】菱形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是对角线
是对角线![]() 所在直线上一点,且
所在直线上一点,且![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]() ,则
,则![]() ____________
____________
【答案】![]() 或
或![]()
【解析】
先利用利用菱形的性质判定△HDG∽△ABG,然后利用菱形的性质和勾股定理求出BD的长,再利用相似三角形的性质即可求出DH的长.
解:①当G点在对角线BD上时,连接AC,交BD于O点,AH交BD,CD于G,H.

∵ABCD是菱形,
∴AC⊥BD,AB∥CD,
∴△HDG∽△ABG,
∴![]() ,
,
∵![]() ,
,
∴DH=DG.
∵AB=3,∠ABC=60°,
∴OA=![]() ,
,
∴OB= ,
,
∵GB=AB,
∴OG=3-![]() ,
,
∴DG=![]() -(3-
-(3-![]() )=
)=![]() ,
,
∴DH=![]() .
.
②当G点在对角线BD延长上时,连接AC,交BD于O点,延长DB使GB=AB,连结GA并延长交CD延长线于H.

∵ABCD是菱形,
∴AC⊥BD,AB∥CD,
∴△HDG∽△ABG,
∴![]() ,
,
∵![]() ,
,
∴DH=DG.
∵AB=3,∠ABC=60°,
∴OA=![]() ,
,
∴OB= ,
,
∴BD=2OB=3![]() ,
,
∵GB=AB,
∴DG=BD+GB=![]() ,
,
∴DH=![]() .
.
故答案为![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在等边![]() 中,点
中,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,直线
,直线![]() 与
与![]() 分别相交于点
分别相交于点![]() ,且
,且![]() .
.
(1)如图(1),写出图中所有与![]() 相似的三角形,并选择其中的一对给予证明;
相似的三角形,并选择其中的一对给予证明;

(2)若直线![]() 向右平移到图(2)、图(3)的位置时,其他条件不变,(1)中的结论是否仍然成立?若成立请写出来(不证明),若不成立,请说明理由;
向右平移到图(2)、图(3)的位置时,其他条件不变,(1)中的结论是否仍然成立?若成立请写出来(不证明),若不成立,请说明理由;
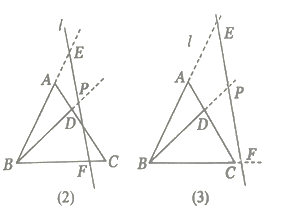
(3)探究:如图(1),当![]() 满足什么条件时(其他条件不变),
满足什么条件时(其他条件不变),![]() ?请写出探究结果,并说明理由(说明:结论中不得含有未标识的字母).
?请写出探究结果,并说明理由(说明:结论中不得含有未标识的字母).
查看答案和解析>>
科目:初中数学 来源: 题型:
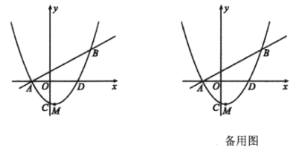
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() ,
,![]() 两点,抛物线
两点,抛物线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴正半轴于
轴正半轴于![]() 点,抛物线的顶点为
点,抛物线的顶点为![]() .
.
(1)求抛物线的解析式;
(2)设点![]() 为直线
为直线![]() 下方的抛物线上一动点,当
下方的抛物线上一动点,当![]() 的面积最大时,求
的面积最大时,求![]() 的面积及点
的面积及点![]() 的坐标;
的坐标;
(3)若点![]() 为
为![]() 轴上一动点,点
轴上一动点,点![]() 在抛物线上且位于其对称轴右侧,当
在抛物线上且位于其对称轴右侧,当![]() 与
与![]() 相似时,求
相似时,求![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
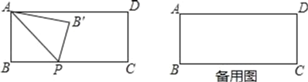
【题目】已知:矩形ABCD,AB=2,BC=5,动点P从点B开始向点C运动,动点P速度为每秒1个单位,以AP为对称轴,把△ABP折叠,所得△AB'P与矩形ABCD重叠部分面积为y,运动时间为t秒.
(1)当运动到第几秒时点B'恰好落在AD上;
(2)求y关于t的关系式,以及t的取值范围;
(3)在第几秒时重叠部分面积是矩形ABCD面积的![]() ;
;
(4)连接PD,以PD为对称轴,将△PCD作轴对称变换,得到△PC'D,当t为何值时,点P、B'、C'在同一直线上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商将一种高档水果放在商场销售,该种水果成本价为10元![]() ,售价为40元
,售价为40元![]() ,每天可销售20
,每天可销售20![]() .调查发现,销售单价每下降1元,每天的销售量将增加5
.调查发现,销售单价每下降1元,每天的销售量将增加5![]() .
.
(1)直接写出每天的销售量ykg与降价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)降价多少元时,每天的销售额![]() 元最大,最大是多少元?(销售额=售价×数量)
元最大,最大是多少元?(销售额=售价×数量)
(3)每销售1![]() 水果,需向商场缴纳柜台费
水果,需向商场缴纳柜台费![]() 元(
元(![]() ),水果商计划租赁柜台20天,为了促销,决定开展“每天降价1元”活动,即从第1天开始,每天的销售单价比前一天下降1元(第1天的销售单价为39元),经测算发现,销售的前11天,每天的利润
),水果商计划租赁柜台20天,为了促销,决定开展“每天降价1元”活动,即从第1天开始,每天的销售单价比前一天下降1元(第1天的销售单价为39元),经测算发现,销售的前11天,每天的利润![]() 元随销售天数
元随销售天数![]() (
(![]() 为正整数)的增大而增大,试确定
为正整数)的增大而增大,试确定![]() 的取值范围.(利润=销售额-成本-柜台费)
的取值范围.(利润=销售额-成本-柜台费)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象相交于A(2,2),B(n,4)两点,连接OA、OB.
的图象相交于A(2,2),B(n,4)两点,连接OA、OB.

(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)在直角坐标系中,是否存在一点P,使以P、A、O、B为顶点的四边形是平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
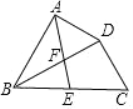
【题目】如图,在四边形ABCD中,BD平分∠ABC,∠BAD=∠BDC=90°,E为BC的中点,AE与BD相交于点F.若BC=4,∠CBD=30°,则DF的长为____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级10个班师生举行传统诗词进校园文艺表演,每班2个节目,有诗词吟诵与诗词吟唱两类节目,学校统计后发现诗词吟诵类节目比诗词吟唱类节目数的2倍少4个
(1)九年级师生表演的诗词吟诵与诗词吟唱类节目数各有多少个?
(2)该校八年级学生有诗词编舞节目参与,在诗词吟诵、诗词吟唱、诗词编舞三类节目中,每个节目的演出用时分别是5分钟,6分钟,8分钟,预计所有演出节目交接用时共花16分钟.若从14:30开始,17:00之前演出结束,问参与的诗词编舞类节目最多能有多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com