
 如图,在等腰三角形DEF中,DE=FE=1,∠DEF=135°.
如图,在等腰三角形DEF中,DE=FE=1,∠DEF=135°.分析 (1)利用等腰直角三角形的性质进而利用锐角三角函数关系得出∠EFD的正切值;
(2)利用等腰三角形DEF的特殊性,得出与其形状相同的三角形即可.
解答  解:(1)延长FE,过点D作DR⊥FE的延长线于点R,
解:(1)延长FE,过点D作DR⊥FE的延长线于点R,
∵等腰三角形DEF中,DE=FE=1,∠DEF=135°,
∴∠DER=45°,
∴DR=ER=$\frac{\sqrt{2}}{2}$,
∴tan∠DFE=$\frac{DR}{RF}$=$\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}+1}$=$\sqrt{2}$-1;
(2)如图所示:以AB为直角边折叠等腰直角三角形,再折叠∠DAG的平分线,即可得出H,G的位置;
∵AB=BG,∠B=90°,
∴∠BAG=∠AGB=45°,
∴∠AGH=135°,
∵∠DAH=∠GAH=22.5°,
∴∠AHG=22.5°,
∴GH=AG,
∴$\frac{DE}{AG}$=$\frac{EF}{GH}$,
又∵∠DEF=∠AGH,
∴△AGH∽△DEF.
点评 此题主要考查了相似三角形的判定与性质以及锐角三角函数关系,得出△AGH各内角度数是解题关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
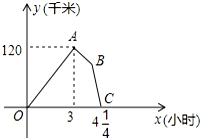 某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后缷完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,则快递车从乙地返回时的速度为90千米/时.
某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后缷完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,则快递车从乙地返回时的速度为90千米/时.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,反比例函数y=-$\frac{4}{x}$的图象与直线y=kx+b交于A(-1,m),B(n,1)两点,则△OAB的面积为( )
如图,反比例函数y=-$\frac{4}{x}$的图象与直线y=kx+b交于A(-1,m),B(n,1)两点,则△OAB的面积为( )| A. | $\frac{11}{2}$ | B. | 4 | C. | $\frac{15}{2}$ | D. | $\frac{13}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在四边形ABCD中,AB∥CD,点E是对角线AC上一点,∠DEC=∠ABC,且CD2=CE•CA.
已知:如图,在四边形ABCD中,AB∥CD,点E是对角线AC上一点,∠DEC=∠ABC,且CD2=CE•CA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线AB与x轴、y轴分别交于B、A两点,线段OA、OB的长是关于x的一元二次方程x2-14x+48=0的两个根(OA<OB)
如图,直线AB与x轴、y轴分别交于B、A两点,线段OA、OB的长是关于x的一元二次方程x2-14x+48=0的两个根(OA<OB)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com