
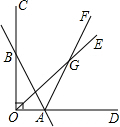
 已知如图,直线AB与OC交于点B,与OD交于点A,射线OE和射线AF交于点G.
已知如图,直线AB与OC交于点B,与OD交于点A,射线OE和射线AF交于点G.分析 (1)根据三角形外角的性质求出∠BAD,求出∠GOA和∠GAD,根据三角形外角性质求出即可;
(2)①根据三角形外角的性质求出∠BAD,求出∠GOA和∠GAD,根据三角形外角性质求出即可;
②根据三角形外角的性质求出∠BAD,求出∠GOA和∠GAD,根据三角形外角性质求出即可;
(3)根据三角形外角的性质求出∠BAD,求出∠GOA和∠GAD,根据三角形外角性质求出即可.
解答 解:(1) ∵∠BOA=90°,∠OBA=36°,
∵∠BOA=90°,∠OBA=36°,
∴∠BAD=∠BOA+∠ABO=126°,
∵AF平分∠BAD,OE平分∠BOA,∠BOA=90°,
∴∠GAD=$\frac{1}{2}$∠BAD=63°,∠EOA=$\frac{1}{2}$∠BOA=45°,
∴∠OGA=∠GAD-∠EOA=63°-45°=18°;
(2)①∵∠BOA=90°,∠OBA=36°,
∴∠BAD=∠BOA+∠ABO=126°,
∵∠BOA=90°,∠GOA=$\frac{1}{3}$∠BOA,∠GAD=$\frac{1}{3}$∠BAD
∴∠GAD=42°,∠EOA=30°,
∴∠OGA=∠GAD-∠EOA=42°-30°=12°;
②∵∠BOA=90°,∠OBA=β,
∴∠BAD=∠BOA+∠ABO=90°+β,
∵∠BOA=90°,∠GOA=$\frac{1}{3}$∠BOA,∠GAD=$\frac{1}{3}$∠BAD
∴∠GAD=30°+$\frac{β}{3}$,∠EOA=30°,
∴∠OGA=∠GAD-∠EOA=$\frac{β}{3}$,
故答案为:$\frac{β}{3}$;
(3)∵∠BOA=90°,∠OBA=β,
∴∠BAD=∠BOA+∠ABO=90°+β,
∵∠BOA=90°,∠GOA=$\frac{1}{n}$∠BOA,∠GAD=$\frac{1}{n}$∠BAD
∴∠GAD=($\frac{90}{n}$)°+$\frac{β}{n}$,∠EOA=($\frac{90}{n}$)°,
∴∠OGA=∠GAD-∠EOA=$\frac{β}{n}$,
故答案为:$\frac{β}{n}$.
点评 本题考查了三角形内角和定理:三角形内角和为180°.也考查了三角形外角性质,求解过程类似.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
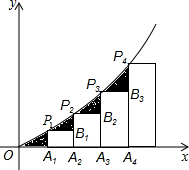 如图已知A1,A2,A3,…An是x轴上的点,且OA1=A1A2=A2A3=A3A4=…=An-1An=1,分别过点A1,A2,A3,…An′作x轴的垂线交二次函数y=$\frac{1}{2}$x2(x>0)的图象于点P1,P2,P3,…Pn,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…依次进行下去,则S3=$\frac{5}{4}$,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn==$\frac{2n-1}{4}$.
如图已知A1,A2,A3,…An是x轴上的点,且OA1=A1A2=A2A3=A3A4=…=An-1An=1,分别过点A1,A2,A3,…An′作x轴的垂线交二次函数y=$\frac{1}{2}$x2(x>0)的图象于点P1,P2,P3,…Pn,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…依次进行下去,则S3=$\frac{5}{4}$,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn==$\frac{2n-1}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com