
【题目】有一张矩形纸片ABCD,![]() ,
,![]() .
.
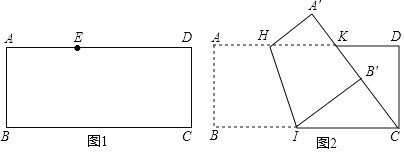
![]() 如图1,点E在这张矩形纸片的边AD上,将纸片折叠,使AB落在CE所在直线上,折痕设为
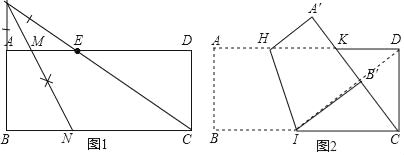
如图1,点E在这张矩形纸片的边AD上,将纸片折叠,使AB落在CE所在直线上,折痕设为![]() 点M,N分别在边AD,BC上
点M,N分别在边AD,BC上![]() ,利用直尺和圆规画出折痕
,利用直尺和圆规画出折痕![]() 不写作法,保留作图痕迹
不写作法,保留作图痕迹![]() ;
;
![]() 如图2,点K在这张矩形纸片的边AD上,
如图2,点K在这张矩形纸片的边AD上,![]() ,将纸片折叠,使AB落在CK所在直线上,折痕为HI,点A,B分别落在点
,将纸片折叠,使AB落在CK所在直线上,折痕为HI,点A,B分别落在点![]() ,
,![]() 处,小明认为
处,小明认为![]() 所在直线恰好经过点D,他的判断是否正确,请说明理由.
所在直线恰好经过点D,他的判断是否正确,请说明理由.
【答案】(1)见解析;(2)小明的判断不正确,理由见解析.
【解析】
(1)延长BA交CE的延长线由G,作∠BGC的角平分线交AD于M,交BC于N,直线MN即为所求;
(2)由△CDK∽△IB′C,推出![]() ,设CB′=3k,IB′=4k,IC=5k,由折叠可知,IB=IB′=4k,可知BC=BI+IC=4k+5k=9,推出k=1,推出IC=5,IB′=4,B′C=3,在Rt△ICB′中,tan∠B′IC=
,设CB′=3k,IB′=4k,IC=5k,由折叠可知,IB=IB′=4k,可知BC=BI+IC=4k+5k=9,推出k=1,推出IC=5,IB′=4,B′C=3,在Rt△ICB′中,tan∠B′IC=![]() ,连接ID,在Rt△ICD中,tan∠DIC=
,连接ID,在Rt△ICD中,tan∠DIC=![]() ,由此即可判断tan∠B′IC≠tan∠DIC,推出B′I所在的直线不经过点D.
,由此即可判断tan∠B′IC≠tan∠DIC,推出B′I所在的直线不经过点D.
(1)如图1所示直线MN即为所求;
(2)小明的判断不正确,理由如下:
如图2,连接ID,
在Rt△CDK中,∵DK=3,CD=4,
∴CK=![]() =5,
=5,
∵AD∥BC,
∴∠DKC=∠ICK,
由折叠可知,∠A′B′I=∠B=90°,
∴∠IB′C=90°=∠D,
∴△CDK∽△IB′C,
∴![]() ,
,
即![]() ,
,
设CB′=3k,IB′=4k,IC=5k,
由折叠可知,IB=IB′=4k,
∴BC=BI+IC=4k+5k=9,
∴k=1,
∴IC=5,IB′=4,B′C=3,
在Rt△ICB′中,tan∠B′IC=![]() ,
,
连接ID,在Rt△ICD中,tan∠DIC=![]() ,
,
∴tan∠B′IC≠tan∠DIC,
∴B′I所在的直线不经过点D.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某品牌笔记本电脑的售价是5000元/台。最近,该商家对此型号笔记本电脑举行促销活动,有两种优惠方案。方案一:每台按售价的九折销售,方案二:若购买不超过5台,每台按售价销售;若超过5台,超过的部分每台按售价的八折销售。设公司一次性购买此型号笔记本电脑x合、
(I)根据题意,填写下表:

(II)设选择方案一的费用为y1元,选择方案二的费用为为y2元,分别写出y1,y2关于x的函数关系式;
(III)当x>15时,该公司采用哪种方案购买更合算?并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCO的顶点B、C在第二象限,点A(﹣3,0),反比例函数y=![]() (k<0)图象经过点C和AB边的中点D,若∠B=α,则k的值为( )
(k<0)图象经过点C和AB边的中点D,若∠B=α,则k的值为( )

A. ﹣4tanαB. ﹣2sinαC. ﹣4cosαD. ﹣2tan
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,C,D,E三点在同一条直线上,连接BD,则下列结论错误的是( )
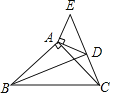
A. △ABD≌△ACE B. ∠ACE+∠DBC=45°
C. BD⊥CE D. ∠BAE+∠CAD=200°
查看答案和解析>>
科目:初中数学 来源: 题型:
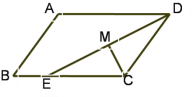
【题目】在平行四边形ABCD中,∠C和∠D的平分线交于M,DM的延长线交AD于E,试猜想:
(1)CM与DE的位置关系?
(2)M在DE的什么位置上?并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售部有营业员16人,销售部为了制定某种商品的月销售定额,统计了这16人某月的销售量如下:
每人销售件数 | 10 | 11 | 12 | 13 | 14 | 15 |
人数 | 1 | 3 | 4 | 3 | 3 | 2 |
(1)这16位销售员该月销售量的众数是_____,中位数是_____,平均数是_____.
(2)若要使75%的营业员都能完成任务,应选什么统计量(平均数、中位数和众数)作为月销售件数的定额?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=a(x+2)2﹣3与y2=![]() (x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结沦:①无论x取何值,y2的值总是正数;②2a=1;③当x=0时,y2﹣y1=4;④2AB=3AC;其中正确结论是( )
(x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结沦:①无论x取何值,y2的值总是正数;②2a=1;③当x=0时,y2﹣y1=4;④2AB=3AC;其中正确结论是( )
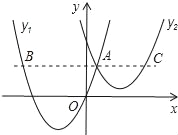
A. ①②B. ②③C. ③④D. ①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com