
����Ŀ�������ڼ䣬֧���������帣����е������帣����������Ϊ5�֣��ֱ�Ϊ��ǿ������г�������Ƹ�������������ҵ�����ӹ��ҡ������������������������������ļ�ֵ�۵ļ�ֵĿ��.
��1��С��һ���˴����ڼ������֧���������帣�����С���ͽ�㶼ȱһ������ҵ������ǡ�ɰְ���һ����������������һ���ˣ������˸������һ����Ϸ����ʤ�ߵõ�����ҵ������
��һ����������������ŷֱ�Ϊ1��2��3��4���ĸ�С����ЩС����˱�������ⶼ��ͬ����С��ҡ�ȣ�
С������Ϸ�����ǣ��Ӻ������������һ��С�������������Ϊ����С������С����ʤ�������н���ʤ�����жϣ�����Ϸ�����С���ͽ�㹫ƽ��˵�����ɣ�
������Ϸ�����ǣ�С���Ӻ������������һ��С���±�����ֺ�Żغ�����ҡ�Ⱥ���ٴӺ����������һ��С�����±������.����������С��ı������ͬΪ������ͬΪż��������С����ʤ������������С��ı������Ϊһ��һż�����н���ʤ�������б�������״ͼ�ķ��������жϴ���Ϸ�����С���ͽ���Ƿ�ƽ.
��2�����帣�������������������ļ�ֵ�۵ļ�ֵĿ��ĸ��˲�������Щ��

���𰸡���1����Ϸ1��С���ͽ���ǹ�ƽ�ģ���Ϸ2��С���ͽ���ǹ�ƽ�ģ���2�����Ƹ�������������ҵ��.
��������
��1����������Ϸ�У��ֱ����С���ͽ���ʤ�ĸ��ʣ����ɵô𰸣�
��2���ֱ�ӹ��ҡ����������������ɵô�.
��1��С������Ϸ���߹���4�ֵȿ��ܽ����һ������С��ı������Ϊ������Ϊż���ĸ���2�֣�
��С����ʤ�ĸ���Ϊ![]() ��
��![]() ������ʤ�ĸ���Ϊ
������ʤ�ĸ���Ϊ![]() ��
��![]() ��
��
����Ϸ1��С���ͽ���ǹ�ƽ�ģ�
������Ϸ������״ͼ���£�

����16�ֿ��������������������С��ı������ͬΪ������ͬΪż���Ĺ���8�֣���������С��ı������Ϊһ��һż�Ľ��Ҳ����8�֣�
��С����ʤ�ĸ���Ϊ![]() ��
��![]() ������ʤ�ĸ���Ϊ
������ʤ�ĸ���Ϊ![]() ��
��![]() ��
��
����Ϸ2��С���ͽ���ǹ�ƽ�ģ�.
��2�����帣���й��Ҳ����ǣ���ǿ�������帣�����������ǣ���г����
���帣���и��˲����ǣ����Ƹ�������������ҵ����


 Сѧ�̲�ȫ��ϵ�д�
Сѧ�̲�ȫ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O��ֱ������CD��AB������Ϊ��P��ֱ��BF��AD�ӳ��߽��ڵ�F���ҡ�AFB����ABC��

��1����֤��ֱ��BF�ǡ�O�����ߣ�
��2����CD��2![]() ��BP��1�����O�İ뾶��
��BP��1�����O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=5��AC=3��BC=4������ABC��A��ʱ�뷽����ת40���õ���ADE����B������·��Ϊ��BD����ͼ����Ӱ���ֵ����Ϊ��������

A. ![]() �Щ�6 B.
��6 B. ![]() �� C.
�� C. ![]() ��3 D.
��3 D. ![]() +��
+��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��O�İ뾶Ϊ1������A��2��0����ֱ���С�O�ڵ�B����y���ڵ�C��
��1�����߶�AB�ij���
��2������ֱ��ACΪͼ���һ�κ����Ľ���ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�������Σ���BCΪ�ױ����������ⲿ������ֱ��������BCE������AE���ֱ�BD��BC�ڵ�F��G�������н��ۣ�����AFB�ס�ABE������ADF�ס�GCE����CG=3BG����AF=EF��������ȷ���У� ��.
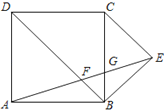
A.�٢�B.�ڢ�C.�٢�D.�ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Բ�ڽ��ı���ABDC��AB����O��ֱ����OD��BC��E��
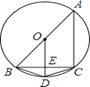
��1����֤����BCD=��CBD��
��2����BE=4��AC=6����DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��AOB��60����OC�ǡ�AOB��ƽ���ߣ���DΪOC��һ�㣬��D��ֱ��DE��OA������Ϊ��E����ֱ��DE��OB�ڵ�F����ͼ��ʾ����DE��2����DF��_____��
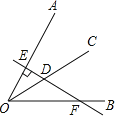
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
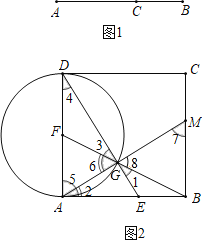
����Ŀ���Ķ����в��ϣ������Ӧ��ѧϰ����:��ͼ��1�����߶�AB����һ��C��C��AB��ΪAC��BC�����߶Σ�����AC��BC����AC��BC��AB�����ϵAC2��BCAB�����C�����߶�AB�Ļƽ�ָ�㣬��ʱ![]() ��
��![]() ��0.618�����ǰ�
��0.618�����ǰ�![]() �����ƽ�ָ��������ǿ��Ը���ͼ��2����ʾ���������ҵ��߶�AB�Ļƽ�ָ�㣬��������Ͳ���֤���������£�
�����ƽ�ָ��������ǿ��Ը���ͼ��2����ʾ���������ҵ��߶�AB�Ļƽ�ָ�㣬��������Ͳ���֤���������£�
��һ������ABΪ����������ABCD��
�ڶ�������ADΪֱ������F��
������������BF���F���ڵ�G��
���IJ�������DG���ӳ���AB���ڵ�E����E�����߶�AB�Ļƽ�ָ�㣮
֤��������AG���ӳ�����BC���ڵ�M��
��ADΪ��F��ֱ����
���AGD��90����
��FΪAD���е㣬
��DF��FG��AF��
���3����4����5����6��
�ߡ�2+��5��90������5+��4��90����
���2����4����3����1��
�ߡ�EBG����GBA��
���EBG�ס�GBA��
��![]() ��
��![]() ��
��
��BG2��BEAB��
����
��1�������������������벿��֤�����̣���ʣ���֤�����̲�������������ʾ��֤��BM��BG��AE��
��2����ѡ����һ�־��й㷺Ӧ�ü�ֵ����ѧ��������ѡ������һ��0.618��Ӧ���˻ƽ�ָ�����Ϊ��ѡ�����ռ�������Ҫ�����ҹ���ѧ������ �����������ѡ�����ĸ���ţ�
A������
B���¾���
C���ղ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������ĺ�����װ�кڡ���������ɫ����50������Щ�����ɫ��������ȫ��ͬ����ӱ���������飬���Ⱥ����Ӻ������������һ���������ɫ���ٰ���Żغ����У������ظ��������̣�����������е�һ��ͳ�����ݣ�
����Ĵ���n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
��������Ĵ���m | 65 | 124 | 178 | 302 | 480 | 600 | 1800 |
���������Ƶ�� | 0.65 | 0.62 | 0.593 | 0.604 | 0.6 | 0.6 | 0.6 |
��1������ƣ���n�ܴ�ʱ�����������Ƶ�ʽ���ӽ��� ��������ȷ��0.1��
��2�����Ӻ������������һ��������������ĸ��ʵĹ���ֵΪ�� ����
��3���Թ��������ڡ���������ɫ������ж��ٸ���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com