
分析 (1)根据判别式即可求出m的范围.
(2)根据根与系数的关系与条件给出的关系式即可列出关于m的等式,从而求出m的值.
解答 解:(1)由题意可知:△=4(m+3)2-4(m2+2)
=4(m2+6m+9)-4(m2+2)
=24m+28>0,
∴m>-$\frac{7}{6}$
(2)由根与系数的关系可知:x1+x2=2(m+3)
x1•x2=m2+2>0,
∵x12+x22=|x1x2|+55,
∴(x1+x2)2-2x1•x2=x1x2+55,
∴4(m+3)2-2(m2+2)=m2+2+55,
∴m2+24m-25=0,
∴m=-25或m=1,
由于m>-$\frac{7}{6}$,
∴m=1
点评 本题考查根与系数的关系,解题的关键是熟练运用根与系数的关系,本题属于中等题型.


科目:初中数学 来源: 题型:解答题
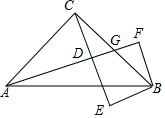 在直角△ABC中,∠ACB=90°,AC=BC,过A点的直线交BC于G,CD⊥AG于D,过B作BE⊥CD交CD的延长线于E.
在直角△ABC中,∠ACB=90°,AC=BC,过A点的直线交BC于G,CD⊥AG于D,过B作BE⊥CD交CD的延长线于E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
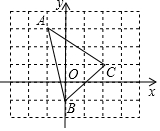 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-1,3),B(0,-1),C(2,1).
如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-1,3),B(0,-1),C(2,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 行驶时间(时) | 1 | 2 | 3 | 4 | 5 |
| 余油量(升) | 55 | 50 | 45 | 40 | 35 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线a、b交于O点,夹角为45°,A、B分别为直线a,b上异于O的点,P为同一平面内不在直线a,b上的定点,且P、A、B不共线,求当△PAB的周长为最小值时,∠APB的度数.
如图,直线a、b交于O点,夹角为45°,A、B分别为直线a,b上异于O的点,P为同一平面内不在直线a,b上的定点,且P、A、B不共线,求当△PAB的周长为最小值时,∠APB的度数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com