
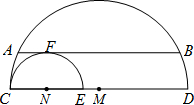
 如图,CD为大半圆M的直径,E为CM上一点,以CE为直径画小半圆N,大半圆M的弦AB与小半圆N相切于点F,且AB∥CD,AB=4,设$\widehat{CD}$、$\widehat{CE}$的长分别为x、y,线段ED的长为z,则z(x+y)的值为8π.
如图,CD为大半圆M的直径,E为CM上一点,以CE为直径画小半圆N,大半圆M的弦AB与小半圆N相切于点F,且AB∥CD,AB=4,设$\widehat{CD}$、$\widehat{CE}$的长分别为x、y,线段ED的长为z,则z(x+y)的值为8π. 分析 过M作MG⊥AB于G,连MB,NF,根据垂径定理得到BG=AG=2,利用勾股定理可得MB2-MG2=22=4,再根据切线的性质有NF⊥AB,而AB∥CD,得到MG=NF,设⊙M,⊙N的半径分别为R,r,则z(x+y)=(CD-CE)(π•R+π•r)=(R2-r2)•2π,即可得到z(x+y)的值.
解答 解:过M作MG⊥AB于G,连MB,NF,如图,
而AB=4,
∴BG=AG=2,
∴MB2-MG2=22=4,
又∵大半圆M的弦与小半圆N相切于点F,
∴NF⊥AB,
∵AB∥CD,
∴MG=NF,
设⊙M,⊙N的半径分别为R,r,
∴z(x+y)=(CD-CE)(π•R+π•r),
=(2R-2r)(R+r)•π,
=(R2-r2)•2π,
=4•2π,
=8π.
故答案为:8π.
点评 本题考查了垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧;也考查了切线的性质和圆的面积公式以及勾股定理.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a7)2=a9 | B. | a7•a2=a14 | ||
| C. | 2a2+3a2=6a5 | D. | (-0.5)2010×22011=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
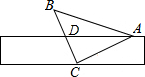 如图,将一个有45°角的三角板的直角顶点C在一张宽为1cm的纸带边沿上,另一个顶点A放在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,则tan∠DAB=2-$\sqrt{3}$.
如图,将一个有45°角的三角板的直角顶点C在一张宽为1cm的纸带边沿上,另一个顶点A放在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,则tan∠DAB=2-$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com