
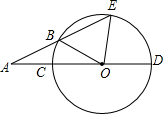
 如图,CD是⊙O的直径,点A在DC的延长线上,AE交⊙O于点B,AB等于⊙O的半径,∠DOE=78°,求∠A的度数.
如图,CD是⊙O的直径,点A在DC的延长线上,AE交⊙O于点B,AB等于⊙O的半径,∠DOE=78°,求∠A的度数. 分析 根据等腰三角形的性质,由AB=OB得到∠A=∠BOA,由OB=OE得到∠E=∠OBE,再根据三角形外角性质得到∠OBE=∠A+∠BOA=2∠A,则∠E=2∠A,然后利用∠DOE=∠A+∠E得到∠A=$\frac{1}{3}$∠DOE=26°.
解答 解:∵AB等于⊙O的半径,
∴AB=OB,
∴∠A=∠BOA,
∵OB=OE,
∴∠E=∠OBE,
∵∠OBE=∠A+∠BOA=2∠A,
∴∠E=2∠A,
∵∠DOE=∠A+∠E,
∴∠DOE=3∠A,
∴∠A=$\frac{1}{3}$∠DOE=$\frac{1}{3}$×78°=26°.
点评 本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了等腰三角形的性质和三角形外角性质.


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{1}{2}}$ | B. | $\sqrt{8}$ | C. | $\sqrt{24}$ | D. | $\sqrt{18}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,小王家在2街与2大道的十字路口,如果用(2,2)→(2,3)→(2,4)→(3,4)→(4,4)→(5,4)表示小王从家到工厂上班的一条路径,那么你能用同样的方式写出由家到工厂小王走的另一条路径吗?
如图,小王家在2街与2大道的十字路口,如果用(2,2)→(2,3)→(2,4)→(3,4)→(4,4)→(5,4)表示小王从家到工厂上班的一条路径,那么你能用同样的方式写出由家到工厂小王走的另一条路径吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
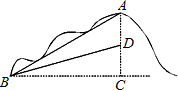 某山区计划修建一条通过小山的公路,经测量,如图,从山底B到山顶A的坡角是30°,斜坡AB长为100米.根据地形,要求修好的公路路面BD的坡度为i=1:5(假定A,D两点处于同一直线上).为了减少工程量,若AD≤20米,则直接开挖修建公路;若AD>20米,就要重新设计.问这段公路是否需要重新设计?
某山区计划修建一条通过小山的公路,经测量,如图,从山底B到山顶A的坡角是30°,斜坡AB长为100米.根据地形,要求修好的公路路面BD的坡度为i=1:5(假定A,D两点处于同一直线上).为了减少工程量,若AD≤20米,则直接开挖修建公路;若AD>20米,就要重新设计.问这段公路是否需要重新设计?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com