
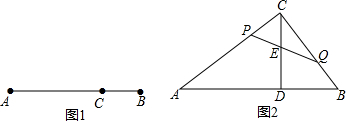
分析 (1)当点C在线段AB上,AC=nAB时,我们称n为点C在线段AB上的点值,记作dC-AB=n,据此进行判断即可;
(2)①根据dP-CA=$\frac{2t}{8}$=$\frac{t}{4}$,dQ-CB=$\frac{6-t}{6}$=1-$\frac{t}{6}$,即可得到m=dP-CA+dQ-CB=$\frac{t}{4}$+1-$\frac{t}{6}$,再根据$\frac{5}{4}$≤m≤$\frac{4}{3}$,即可得到不等式$\frac{5}{4}$≤$\frac{t}{4}$+1-$\frac{t}{6}$≤$\frac{4}{3}$,进而解得3≤t≤4;
②根据dP-CA=$\frac{m}{2}$,dP-CA+dQ-CB=m,可得dP-CA=dQ-CB,即$\frac{CP}{CA}$=$\frac{CQ}{CB}$,进而得出$\frac{2t}{8}$=$\frac{6-t}{6}$,求得t=2.4,再根据$\frac{CP}{CA}$=$\frac{CQ}{CB}$,∠ACB=∠PCQ,判定△ACB∽△PCQ,进而得到PQ∥AB,得出$\frac{CE}{CD}$=$\frac{CP}{CA}$,即可得到dE-CD=dP-CA=$\frac{2t}{8}$=0.6;
③分两种情况:当PQ∥AB时,则有dE-CD=dP-CA=dQ-CB=$\frac{m}{2}$,由②可得,t=2.4;当PQ与AB不平行时,过点P,Q分别作PM⊥CD于点M,QN⊥CD于点N,根据dE-CD=$\frac{m}{2}$,dP-CA+dQ-CB=m,推理可得△PME≌△QNE,即可得出PM=QN,最后根据PM=PC×sin∠ACD=2t×sin∠B=$\frac{8t}{5}$,QN=QC×sin∠BCD=(6-t)sin∠A=$\frac{3}{5}$(6-t),得到关于t的方程$\frac{8t}{5}$=$\frac{3}{5}$(6-t),即可得出t=$\frac{18}{11}$.
解答 解:(1)∵点C在线段AB上,若dC-AB=$\frac{2}{3}$,
∴AC=$\frac{2}{3}$AB,即$\frac{AC}{AB}$=$\frac{2}{3}$;
∵AC=3BC,
∴AC=$\frac{3}{4}$AB,即dC-AB=$\frac{3}{4}$,
故答案为:$\frac{2}{3}$,$\frac{3}{4}$;
(2)①在△ABC中,∠ACB=90°,AB=10,BC=6,
∴AC=8,
∵dP-CA=$\frac{2t}{8}$=$\frac{t}{4}$,dQ-CB=$\frac{6-t}{6}$=1-$\frac{t}{6}$,
∴m=dP-CA+dQ-CB=$\frac{t}{4}$+1-$\frac{t}{6}$,
又∵$\frac{5}{4}$≤m≤$\frac{4}{3}$,
∴$\frac{5}{4}$≤$\frac{t}{4}$+1-$\frac{t}{6}$≤$\frac{4}{3}$,
解得3≤t≤4;
②∵dP-CA=$\frac{m}{2}$,dP-CA+dQ-CB=m,
∴dP-CA=dQ-CB,
∴$\frac{CP}{CA}$=$\frac{CQ}{CB}$,
∴$\frac{2t}{8}$=$\frac{6-t}{6}$,
解得t=2.4,
∵$\frac{CP}{CA}$=$\frac{CQ}{CB}$,∠ACB=∠PCQ,
∴△ACB∽△PCQ,
∴∠A=∠CPQ,
∴PQ∥AB,
∴$\frac{CE}{CD}$=$\frac{CP}{CA}$,
∴dE-CD=dP-CA=$\frac{2t}{8}$=0.6;
③分两种情况:
当PQ∥AB时,则有dE-CD=dP-CA=dQ-CB=$\frac{m}{2}$,
由②可得,t=2.4;
当PQ与AB不平行时,过点P,Q分别作PM⊥CD于点M,QN⊥CD于点N,如图所示,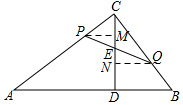
则有PM∥QN∥AB,且点M,N,E不重合,
∴$\frac{CP}{AC}$=$\frac{CM}{CD}$,$\frac{CQ}{CB}$=$\frac{CN}{CD}$,
∵dE-CD=$\frac{m}{2}$,dP-CA+dQ-CB=m,
∴dP-CA+dQ-CB=2dE-CD,
∴$\frac{CP}{AC}$+$\frac{CQ}{CB}$=2$\frac{CE}{CD}$,即$\frac{CM}{CD}$+$\frac{CN}{CD}$=2$\frac{CE}{CD}$,
∴CM+CN=2CE,即点E是MN的中点,
∴EN=EM,
又∵∠PME=∠QNE,∠PEM=∠QEN,
∴△PME≌△QNE,
∴PM=QN,
∵PM=PC×sin∠ACD=2t×sin∠B=$\frac{8t}{5}$,QN=QC×sin∠BCD=(6-t)sin∠A=$\frac{3}{5}$(6-t),
∴$\frac{8t}{5}$=$\frac{3}{5}$(6-t),
解得t=$\frac{18}{11}$,
综上所述,t的值为2.4或$\frac{18}{11}$.
点评 本题属于相似形综合题,主要考查了相似三角形的判定与性质,全等三角形的判定与性质以及解直角三角形的综合应用,解决问题③的关键是作辅助线构造全等三角形,依据全等三角形对应边相等,列方程求解,解题时注意分类思想的运用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a-b)2=a2-b2 | B. | (2a+b)(-2a+b)=2a2-b2 | ||
| C. | (a+1)(a-2)=a2-2 | D. | (-a-b)2=a2+2ab+b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
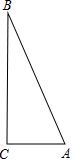 实践操作:如图,△ABC是直角三角形,∠ACB=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母.(保留作图痕迹,不写作法)
实践操作:如图,△ABC是直角三角形,∠ACB=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母.(保留作图痕迹,不写作法)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$的图象的两个交点.
如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$的图象的两个交点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
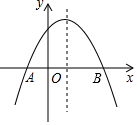 如图,抛物线y=ax2+bx+c,与x轴交于点A(-1,0),顶点坐标为(1,n),与y轴交点在(0,2)、(0,3)之间(包含端点),有下列结论:①abc>0;②4ac-b2>0;③当x=3时,y=0;④3a+b>0;⑤-1≤a≤-$\frac{2}{3}$,;⑥$\frac{8}{3}$≤n≤4,其中正确的有( )
如图,抛物线y=ax2+bx+c,与x轴交于点A(-1,0),顶点坐标为(1,n),与y轴交点在(0,2)、(0,3)之间(包含端点),有下列结论:①abc>0;②4ac-b2>0;③当x=3时,y=0;④3a+b>0;⑤-1≤a≤-$\frac{2}{3}$,;⑥$\frac{8}{3}$≤n≤4,其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
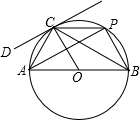 如图,点C是半径长为3的⊙O上任意一点,AB为直径,AC=3,过点C作⊙O的切线DC,点P为⊙O优弧AC上不与A、C重合的一个动点,点P从点C出发以每秒π个单位的速度顺时针匀速运动,到达点A停止运动.
如图,点C是半径长为3的⊙O上任意一点,AB为直径,AC=3,过点C作⊙O的切线DC,点P为⊙O优弧AC上不与A、C重合的一个动点,点P从点C出发以每秒π个单位的速度顺时针匀速运动,到达点A停止运动.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com