
����ͼ��ʾ���������ֱַ���1��2��3��4�������˿��Ʊ��泯�ϣ�ϴ�Ⱥ���������ϣ���1�������� �����һ���ƣ�����������ż���ĸ����� ��
�����һ���ƣ�����������ż���ĸ����� ��
��2�����������������ƣ��������������ֵĺ���5�ĸ����� ��
��3���ȴ���������һ���ƣ�������������Ϊʮλ�ϵ����֣�Ȼ���ƷŻز�����ϴ�ȣ��������ȡһ�ţ�������������Ϊ��λ�ϵ����֣����û���״ͼ���б��ķ�������ɵ���λ��ǡ����4�ı����ĸ��ʣ�


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ�������£�С����������ͼ���߶�AB��ʾ�����ڵ����ϵ�Ӱ����ͼ���߶�BC��ʾ���߶�DE��ʾ��˵ĸߣ��߶�FG��ʾһ�¸�ǽ��
��1��������ͼ�л��������ͬһʱ�������������γɵ�Ӱ�ӣ�
��2�����С��������AB=1.6m������Ӱ��BC=2.4m����˵ĸ�DE=15m��������ǽ�ľ���EG=16m���������˵�Ӱ������ǽ�ϵij��ȣ�

��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�������� ����ƽ��1����λ��Ȼ������ƽ��3����λ����ƽ�ƺ������ߵĽ���ʽΪ�� ��. A
����ƽ��1����λ��Ȼ������ƽ��3����λ����ƽ�ƺ������ߵĽ���ʽΪ�� ��. A ��
�� B��
B��
C��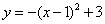 D��
D��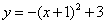
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ���ڷ���������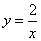 ��
�� ����ͼ���ϣ��е�
����ͼ���ϣ��е� �����ǵĺ���������Ϊ1��2��3��4���ֱ����Щ����
�����ǵĺ���������Ϊ1��2��3��4���ֱ����Щ����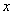 ����
����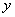 ��Ĵ��ߣ�ͼ�������ɵ���Ӱ���ֵ��������������Ϊ
��Ĵ��ߣ�ͼ�������ɵ���Ӱ���ֵ��������������Ϊ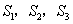 ����
���� ��
��


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����x2=4x�Ľ��ǣ�������
�� A�� x=4 B�� x=2 C�� x=4��x=0 D�� x=0
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪һ�����ݣ�12��5��9��5��14������˵������ȷ���ǣ�������
�� A�� ������5 B�� ��λ����9 C�� ������5 D�� ƽ������9
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
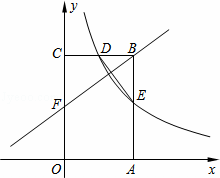
��ͼ������OABC�Ķ���A��C�ֱ���x���y���ϣ���B������Ϊ��2��3����˫����y= ��x��0����ͼ��BC���е�D������AB���ڵ�E������DE��
��x��0����ͼ��BC���е�D������AB���ڵ�E������DE��
��1����k��ֵ����E�����ꣻ
��2������F��OC����һ�㣬�ҡ�FBC�ס�DEB����ֱ��FB�Ľ���ʽ��
��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
������x��һԪ���η��̵�������Ϊx1=1��x2=2������������ǣ� C ��
A��x2+3x��2=0 B��x2+3x+2=0 C��x2��3x+2=0 D��x2��2x+3=0
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com