
����Ŀ��ij��Ʒ�������۽���Ϊ40Ԫ/���ƻ�����г����鷢�֣�����ÿ����50Ԫ�ļ۸����ۣ�ƽ��ÿ������90�䣬�۸�ÿ���1Ԫ��ƽ��ÿ��������3�䣬��ÿ��ƻ�������ۼ�Ϊx��Ԫ����x��50��ʱ��ƽ��ÿ�����������Ϊw��Ԫ��.
��1����w��x֮��ĺ�����ϵʽ��
��2����ÿ��ƻ�������ۼ�Ϊ����Ԫʱ�����Ի����������������Ϊ����Ԫ��
��3���ٽ����ڣ�Ϊ�ȶ��г�����۲��Ź涨ÿ��ƻ���ۼ۲��ø���58Ԫ�����ʱƽ��ÿ���õ���������Ƕ���Ԫ��
���𰸡���1��w��x֮��ĺ�����ϵʽΪw=![]() ��
��
��2��ÿ��ƻ�������ۼ�Ϊ60Ԫʱ�����Ի������������������1200Ԫ��
��3����x=58ʱ��w�����ֵ��w���=1188����ʱƽ��ÿ���õ����������1188Ԫ��
��������
��1�����������ó�ƽ��ÿ����������y�������ۼ�x��Ԫ/�䣩֮��ĺ�����ϵʽΪy��903��x50����Ȼ������������������������ۼ����ۣ����г�ƽ��ÿ�����������w��Ԫ�������ۼ�x��Ԫ/�䣩֮��ĺ�����ϵʽ���ɣ�
��2��������������Ա�����ȡֵ��Χ��Ȼ�������1���ж��κ�������ֵ���ɣ�
��3�������������x��ȡֵ��Χ�������ö��κ������������ɵã�
�⣺��1��������ã�y��903��x50����
��w=![]() =
=![]() =
=![]() ��
��
��w��x֮��ĺ�����ϵʽΪw=![]() ��
��
��2����![]() ����
����![]() ��
��
��![]() ��
��
�߶��κ���w=![]() �Ķ��������ǣ�60��1200����
�Ķ��������ǣ�60��1200����
�൱x=60 ʱ��w�����ֵ��w���=1200��
��ÿ��ƻ�������ۼ�Ϊ60Ԫʱ�����Ի������������������1200Ԫ��
��3����![]() ����
����![]() ��58��
��58��
��![]() ��58��
��58��
�߶��κ���w=![]() �У�
�У�![]() ���������£��Գ�����ֱ��
���������£��Գ�����ֱ��![]() ��
��
�൱![]() ʱ��w��ֵ��xֵ�����������
ʱ��w��ֵ��xֵ�����������
�൱x=58ʱ��w�����ֵ��w���=1188��
�𣺴�ʱƽ��ÿ���õ����������1188Ԫ��


 ȫ�ܲ��һ���þ�ϵ�д�
ȫ�ܲ��һ���þ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y1=��x+4��y2=![]() x+b����˫����y=
x+b����˫����y=![]() ���ڵ�A��1��m����������ֱ�߷ֱ���x�ύ��B��C���㣮
���ڵ�A��1��m����������ֱ�߷ֱ���x�ύ��B��C���㣮
��1����y��x֮��ĺ�����ϵʽ��
��2��ֱ��д����x��0ʱ������ʽ![]() x+b��
x+b��![]() �Ľ⼯��
�Ľ⼯��
��3������P��x���ϣ�����AP����ABC������ֳ�1��3�����֣����ʱ��P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������Ŀڴ���װ��4���ֱ������1��2��3��4��С�����ǵ���״����С��ȫ��ͬ��С���ȴӿڴ����������һ��С�������Ϊx��Сӱ��ʣ�µ�3�������������һ��С�������Ϊy������ȷ���˵�P�����꣨x��y����
��1��С������������3��С��ĸ����Ƕ��٣���
��2���������б�������״ͼ����ʾ����x��yȷ���ĵ�P��x��y�����п��ܵĽ����
��3�����P��x��y���ں���y=��x+5ͼ���ϵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
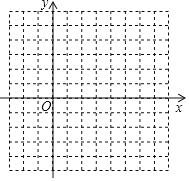
����Ŀ����֪������![]()
![]() �Գ���Ϊ______����������Ϊ______��
�Գ���Ϊ______����������Ϊ______��
![]() ������ϵ��������㷨�����������ߣ�
������ϵ��������㷨�����������ߣ�
x |
| ______ | ______ | ______ | ______ | ______ |
|
y |
| ______ | ______ | ______ | ______ | ______ |
|
![]() ����������x�ύ��ΪA��B����
����������x�ύ��ΪA��B����![]() ���������ϣ���
���������ϣ���![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������y=kx(k��0)��ͼ����P(2,3),��ú�����ͼ���ĵ���( )
A.(3,2)B.(1,6)C.(2,3)D.(1,6)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ABC�ǵȱ������Σ���D��E�ֱ��ڱ�BC��AC�ϣ���BD=CE��AD��BE�ཻ�ڵ�F.
��1����֤����ABD�ա�BCE
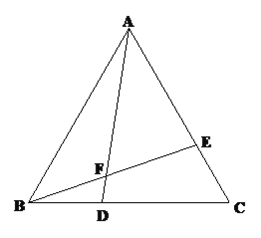
��2����֤�� ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
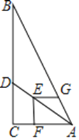
����Ŀ����ͼ����Rt��ABC�У���ACB=90����AC=6��BC=12����D�ڱ�BC�ϣ���E���߶�AD�ϣ�EF��AC�ڵ�F��EG��EF��AB�ڵ�G����EF = EG����CD�ij�Ϊ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�BE��FC��CF��2FD��AE��BF���ڵ�G������AF���������н��ۣ���AE��BF�� ��AE��BF�� ��BG��![]() GE�� ��S�ı���CEGF��S��ABG��������ȷ�ĸ���Ϊ��������
GE�� ��S�ı���CEGF��S��ABG��������ȷ�ĸ���Ϊ��������

A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
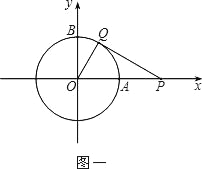
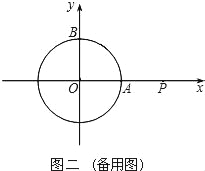
����Ŀ��������ԭ��ΪԲ�ģ�1Ϊ�뾶��Բ�ֱ�x��y����������ڵ�A��B��
��1����ͼһ������P�ӵ�A����������x�����������˶������ͬʱ������Q�ӵ�B����������Բ�ܰ�˳ʱ�뷽�������˶�������Q���˶��ٶȱȵ�P���˶��ٶ���������1����P�˶����㣨2��0������ʱPQǡ������O�����ߣ�����OQ������QOP�Ĵ�С��
��2������Q���գ�1���еķ�����ٶȼ����˶�����Pͣ���ڵ㣨2��0�������������Q�پ���5���ֱ��PQ����O�صõ��ҳ���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com