练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

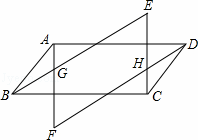
    如图，四边形ABCD是平行四边形，作AF∥CE，BE∥DF，AF交BE与G点，交DF与F点，CE交DF于H点、交BE于E点．

    求证：△EBC≌△FDA．


    证明：∵四边形ABCD是平行四边形，

    ∴AD=BC，AD∥BC，

    ∵AF∥CE，BE∥DF，

    ∴四边形BHDK和四边形AMCN是平行四边形，

    ∴∠FAD=∠ECB，∠ADF=∠EBC，

    在△EBC和△FDA中，

    ∴△EBC≌△FDA．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    计算（﹣1）2+20﹣|﹣3|的值等于（　　）

    　

    A．

    ﹣1

    B．

    0

    C．

    1

    D．

    5

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图6，一渔船由西往东航行，在A点测得海岛C位于北偏东60°的方向，前进20海里到达B点，此时，测得海岛C位于北偏东30°的方向，则海岛C到航线AB的距离CD等于       海里.

     


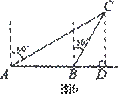    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列说法中不正确的是（　　）

    　

    A．

    抛掷一枚硬币，硬币落地时正面朝上是随机事件

    　

    B．

    把4个球放入三个抽屉中，其中一个抽屉中至少有2个球是必然事件

    　

    C．

    任意打开七年级下册数学教科书，正好是97页是确定事件

    　

    D．

    一个盒子中有白球m个，红球6个，黑球n个（每个除了颜色外都相同）．如果从中任取一个球，取得的是红球的概率与不是红球的概率相同，那么m与n的和是6

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，圆锥的表面展开图由一扇形和一个圆组成，已知圆的面积为100π，扇形的圆心角为120°，这个扇形的面积为　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


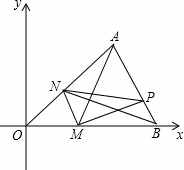
    如图，在平面直角坐标系中，△AOB的三个顶点的坐标分别是A（4，3），O（0，0），B（6，0）．点M是OB边上异于O，B的一动点，过点M作MN∥AB，点P是AB边上的任意点，连接AM，PM，PN，BN．设点M（x，0），△PMN的面积为S．

    （1）求出OA所在直线的解析式，并求出点M的坐标为（1，0）时，点N的坐标；

    （2）求出S关于x的函数关系式，写出x的取值范围，并求出S的最大值；

    （3）若S：S△ANB=2：3时，求出此时N点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某中学随机调查了15名学生，了解他们一周在校参加体育锻炼时间，列表如下：

    锻炼时间（小时）

    5

    6

    7

    8

    人数

    2

    6

    5

    2

    则这15名同学一周在校参加体育锻炼时间的中位数和众数分别是（　　）

    　

    A．

    6，7

    B．

    7，7

    C．

    7，6

    D．

    6，6

    查看答案和解析>>

    科目：初中数学 来源： 题型：


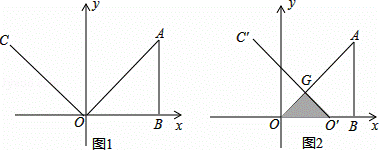
    如图1，在平面直角坐标系中，AB=OB=8，∠ABO=90°，∠yOC=45°，射线OC以每秒2个单位长度的速度向右平行移动，当射线OC经过点B时停止运动，设平行移动x秒后，射线OC扫过Rt△ABO的面积为y．

    （1）求y与x之间的函数关系式；

    （2）当x=3秒时，射线OC平行移动到O′C′，与OA相交于G，如图2，求经过G，O，B三点的抛物线的解析式；

    （3）现有一动点P在（2）中的抛物线上，试问点P在运动过程中，是否存在三角形POB的面积S=8的情况？若存在，求出点P的坐标，若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    |﹣8|=

    查看答案和解析>>

    同步练习册答案