
分析 先用多项式乘以多项式的运算法则展开求它们的积,并且把m、n看作常数合并关于x的同类项,令x2及x3的系数为0,构造关于m、n的二元一次方程组,求出m、n的值即可得答案.
解答 解:(x2-4x+n)(x2+mx+8)=x4+(m-4)x3+(8+n-4m)x2+(mn-32)x+8n,
又∵结果不含x2和x3的项,
∴$\left\{\begin{array}{l}{m-4=0}\\{8+n-4m=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=4}\\{n=8}\end{array}\right.$.
∴m+n=12,
故答案为:12.
点评 本题主要考查了多项式乘多项式的运算,当多项式中不含有哪一项时,即哪一项的系数为0.


科目:初中数学 来源: 题型:解答题
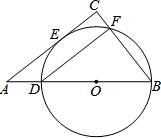 如图,在Rt△ACB中,∠C=90°,D是AB上一点,以BD为直径的⊙O切AC于点E,交BC于点F,连接DF.
如图,在Rt△ACB中,∠C=90°,D是AB上一点,以BD为直径的⊙O切AC于点E,交BC于点F,连接DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
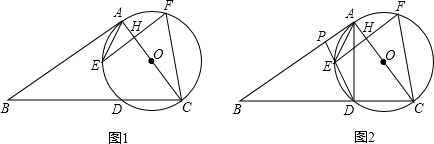
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com