
| A.它的开口方向是向下 | B.当x<-1时,y随x的增大而减小 |
| C.它的顶点坐标是(2,3) | D.当x=0时,y有最大值是3 |
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源:不详 题型:解答题
 的一元二次函数
的一元二次函数 (
( )的图象与
)的图象与 轴相交于
轴相交于 、
、 两点(点
两点(点 在点
在点 的左侧),与
的左侧),与 轴交于点
轴交于点 ,且
,且 ,顶点为
,顶点为 .
.
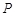 为线段
为线段 上的一个动点,过点
上的一个动点,过点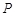 作
作 轴的垂线
轴的垂线 ,垂足为
,垂足为 .若
.若 ,
, 的面积为
的面积为 ,求
,求 关于
关于 的函数关系式,并写出
的函数关系式,并写出 的取值范围;
的取值范围; 点坐标是 时,
点坐标是 时, 为直角三角形.
为直角三角形.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
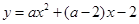 过点
过点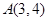 .
.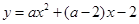 在直线
在直线 下方的部分沿直线
下方的部分沿直线 翻折,图象其余的部分保持不变,得到的新函数图象记为
翻折,图象其余的部分保持不变,得到的新函数图象记为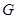 .点
.点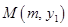 在图象
在图象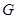 上,且
上,且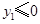 .
.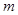 的取值范围;
的取值范围;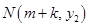 也在图象
也在图象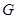 上,且满足
上,且满足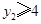 恒成立,则
恒成立,则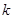 的取值范围为 .
的取值范围为 .查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的图象与
的图象与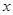 轴交于B、C两点(点B在点C的左侧),一次函数
轴交于B、C两点(点B在点C的左侧),一次函数 的图象经过点B和二次函数图象上另一点A. 点A的坐标(4 ,3),
的图象经过点B和二次函数图象上另一点A. 点A的坐标(4 ,3),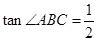 .
.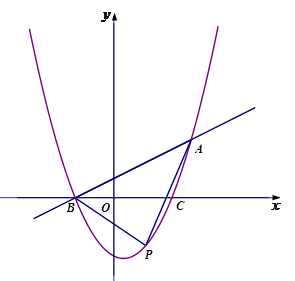
 面积S的最大值并求出此时点P的坐标;
面积S的最大值并求出此时点P的坐标;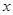 轴距离的
轴距离的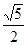 倍,求点M的坐标.
倍,求点M的坐标.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 价格y1(元/件) | 56 | 58 | 60 | 62 | 64 | 66 | 68 | 70 | 72 |

 (1≤x≤9,且x取整数),10至12月的销售量p2(万件)与月份x满足函数关系式
(1≤x≤9,且x取整数),10至12月的销售量p2(万件)与月份x满足函数关系式 (10≤x≤12,且x取整数)。求去年哪个月销售该配件的利润最大,并求出这个最大利润;
(10≤x≤12,且x取整数)。求去年哪个月销售该配件的利润最大,并求出这个最大利润;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB =" 2OA" = 4.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB =" 2OA" = 4.
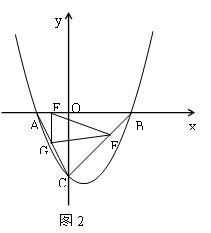
 个单位长度的速度向终点C运动,过点E作EG//y轴,交AC于点G(如图2).若E、F两点同时出发,运动时间为t.则当t为何值时,△EFG的面积是△ABC的面积的
个单位长度的速度向终点C运动,过点E作EG//y轴,交AC于点G(如图2).若E、F两点同时出发,运动时间为t.则当t为何值时,△EFG的面积是△ABC的面积的 ?
?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com