
| A. | 乙>甲>丙 | B. | 乙>丙>甲 | C. | 甲>乙>丙 | D. | 甲>丙>乙 |
分析 首先把360分解质因数,可得360=2×2×2×3×3×5;然后根据甲乙丙化为最简分数后的分子分别为6、15、10,6=2×3,可得化简后的甲的分母中不含有因数2、3,只能为5,即化简后的甲为$\frac{6}{5}$;再根据15=3×5,可得化简后的乙的分母中不含有因数3、5,只能为2,4或8;再根据10=2×5,可得化简后的丙的分母中不含有因数2、5,只能为3或9;最后根据化简后的三个数的分母的最小公倍数为360,甲的分母为5,可得乙、丙的最小公倍数是360÷5=72,再根据化简后的乙、丙两数的分母的取值情况分类讨论,判断出化简后的乙、丙两数的分母各是多少,进而求出化简后的甲乙丙各是多少,再根据分数大小比较的方法判断即可.
解答 解:360=2×2×2×3×3×5;
因为6=2×3,
所以化简后的甲的分母中不含有因数2、3,只能为5,
即化简后的甲为$\frac{6}{5}$;
因为15=3×5,
所以化简后的乙的分母中不含有因数3、5,只能为2,4或8;
因为10=2×5,
所以化简后的丙的分母中不含有因数2、5,只能为3或9;
因为化简后的三个数的分母的最小公倍数为360,甲的分母为5,
所以乙、丙的最小公倍数是360÷5=72,
(1)当乙的分母是2时,丙的分母是9时,
乙、丙的最小公倍数是:2×9=18,
它不满足乙、丙的最小公倍数是72;
(2)当乙的分母是4时,丙的分母是9时,
乙、丙的最小公倍数是:4×9=36,
它不满足乙、丙的最小公倍数是72;
所以乙的分母只能是8,丙的分母只能是9,
此时乙、丙的最小公倍数是:8×9=72,
所以化简后的乙是$\frac{15}{8}$,丙是$\frac{10}{9}$,
因为$\frac{15}{8}>\frac{6}{5}>\frac{10}{9}$,
所以乙>甲>丙.
故选:A.
点评 (1)此题主要考查了最简分数的特征,以及几个数的最小公倍数的求法,考查了分类讨论思想的应用,要熟练掌握,解答此题的关键是分别求出化简后的甲、乙、丙的分母各是多少,进而求出化简后的甲乙丙各是多少.
(2)此题还考查了分数大小比较的方法,要熟练掌握.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
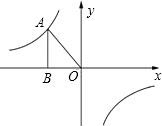 如图所示,已知反比例函数y=$\frac{k}{x}$(k<0)的图象经过点A(-$\sqrt{3}$,m),过点A作AB⊥x轴于点B,且△AOB的面积为2$\sqrt{3}$.
如图所示,已知反比例函数y=$\frac{k}{x}$(k<0)的图象经过点A(-$\sqrt{3}$,m),过点A作AB⊥x轴于点B,且△AOB的面积为2$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com