
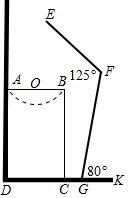
 如图是小强洗漱时的侧面示意图,洗漱台(矩形ABCD)靠墙摆放,高AD=80cm,宽AB=48cm,小强身高166cm,下半身FG=100cm,洗漱时下半身与地面成80°(∠FGK=80°),身体前倾成125°(∠EFG=125°),脚与洗漱台距离GC=15cm(点D,C,G,K在同一直线上).
如图是小强洗漱时的侧面示意图,洗漱台(矩形ABCD)靠墙摆放,高AD=80cm,宽AB=48cm,小强身高166cm,下半身FG=100cm,洗漱时下半身与地面成80°(∠FGK=80°),身体前倾成125°(∠EFG=125°),脚与洗漱台距离GC=15cm(点D,C,G,K在同一直线上).分析 (1)过点F作FN⊥DK于N,过点E作EM⊥FN于M.求出MF、FN的值即可解决问题;
(2)求出OH、PH的值即可判断;
解答 解:(1)过点F作FN⊥DK于N,过点E作EM⊥FN于M.
∵EF+FG=166,FG=100,
∴EF=66,
∵∠FGK=80°,
∴FN=100•sin80°≈98,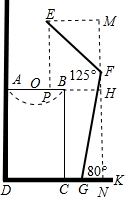
∵∠EFG=125°,
∴∠EFM=180°-125°-10°=45°,
∴FM=66•cos45°=33$\sqrt{2}$≈46.53,
∴MN=FN+FM≈144.5,
∴此时小强头部E点与地面DK相距约为144.5cm.
(2)过点E作EP⊥AB于点P,延长OB交MN于H.
∵AB=48,O为AB中点,
∴AO=BO=24,
∵EM=66•sin45°≈46.53,
∴PH≈46.53,
∵GN=100•cos80°≈17,CG=15,
∴OH=24+15+17=56,OP=OH-PH=56-46.53=9.47≈9.5,
∴他应向前9.5cm.
点评 本题考查直角三角形的应用,锐角三角函数等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | 3,2 | B. | 3,4 | C. | 5,2 | D. | 5,4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
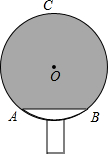 如图,小明自制一块乒乓球拍,正面是半径为8cm的⊙O,$\widehat{AB}$=90°,弓形ACB(阴影部分)粘贴胶皮,则胶皮面积为(32+48π)cm2.
如图,小明自制一块乒乓球拍,正面是半径为8cm的⊙O,$\widehat{AB}$=90°,弓形ACB(阴影部分)粘贴胶皮,则胶皮面积为(32+48π)cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
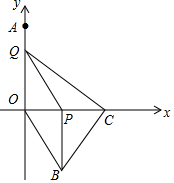 如图,在平面直角坐标系中,点A (0,4).动点P从原点O出发,沿x轴正方向以每秒2个单位的速度运动,同时动点Q从点A出发,沿y轴负方向以每秒1个单位的速度运动,以QO、QP为邻边构造平行四边形OQPB,在线段OP的延长线长取点C,使得PC=2,连接BC、CQ.设点P、Q运动的时间为t(0<t<4)秒.
如图,在平面直角坐标系中,点A (0,4).动点P从原点O出发,沿x轴正方向以每秒2个单位的速度运动,同时动点Q从点A出发,沿y轴负方向以每秒1个单位的速度运动,以QO、QP为邻边构造平行四边形OQPB,在线段OP的延长线长取点C,使得PC=2,连接BC、CQ.设点P、Q运动的时间为t(0<t<4)秒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com