
【题目】如图所示,点A, 0, B在同一条直线上,OD平分∠AOC, OE平分∠BOC.
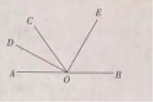
(1)若∠B0D=160°,求∠BOE的度数;
(2) 若∠COE比∠COD多60°.求∠COE的度数.
【答案】(1)∠BOE=70°;(2)∠COE=75°.
【解析】
(1)利用角平分线的性质求出∠DOE的度数,再根据∠BOD=160°求∠BOE的度数;
(2)根据∠COE比∠COD多60°可得∠COE =60°+∠COD,结合(1)∠COE+∠COD=90°,即可求出∠COE的度数
解:(1)如图,因为OD是∠AOC的平分线,
所以∠COD=![]() ∠AOC,
∠AOC,
又因为OE是∠BOC的平分线,
所以∠COE=![]() ∠BOC.
∠BOC.
所以∠DOE=∠COD+∠COE=![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() ∠AOB=90°,
∠AOB=90°,
因为∠BOD=160°,
所以∠BOE=∠BOD-∠DOE=160°-90°=70°.
(2)由(1)可知,∠DOE=90°.
因为∠COE比∠COD多60°,
所以∠COE =60°+∠COD,
因为∠COE+∠COD=90°,
所以60°+∠COD +∠COD=90°
即∠COD=15°,∠COE=75°.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
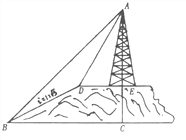
【题目】如图,小山的顶部是一块平地,在这块平地上有一高压输电的铁架,小山的斜坡的坡度![]() ,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为
,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为![]() ,在山坡的坡顶D处测得铁架顶端A的仰角为
,在山坡的坡顶D处测得铁架顶端A的仰角为![]() ,(1)求小山的高度;(2)求铁架的高度。(结果保留根号)
,(1)求小山的高度;(2)求铁架的高度。(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第16届省运会在我市隆重举行,推动了我市各校体育活动如火如荼的开展,在某校射箭队的一次训练中,甲,乙两名运动员前5箭的平均成绩相同,教练将两人的成绩绘制成如下尚不完整的统计图表.
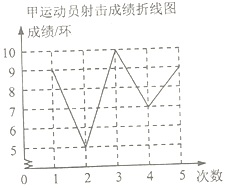
乙运动员成绩统计表(单位:环)
第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
8 | 10 | 8 | 6 |
|
(1)甲运动员前5箭射击成绩的众数是 环,中位数是 环;
(2)求乙运动员第5次的成绩;
(3)如果从中选择一个成绩稳定的运动员参加全市中学生比赛,你认为应选谁去?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位农民带上若干千克自产的土豆进城出售.为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数x与他手中持有的钱数y(含备用零钱)的关系如图所示,结合图象回答下列问题:

(1)农民自带的零钱是多少?
(2)求降价前农民手中的钱数y与售出的土豆千克数x的函数关系式;
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家将一种电视机按进价提高35%后定价,然后打出“九折酬宾,外送50元出租车费”的广告,结果每台电视机获利208元.
(1)求每台电视机的进价;
(2)另有一家商家出售同类产品,按进价提高40%,然后打出“八折酬宾”的广告,如果你想买这种产品,应选择哪一个商家?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,点E在边CD上,连结AE、BE.给出下列五个关系式:①AD∥BC;②DE=CE;③∠1=∠2;④∠3=∠4;⑤AD+BC=AB.将其中的三个关系式作为题设,另外两个作为结论,构成一个命题.
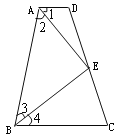
⑴用序号写出一个真命题(书写形式如:如果×××,那么××);并给出证明;
⑵用序号再写出三个真命题(不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市城市居民用电收费方式有以下两种:
(甲)普通电价:全天0.53元/度;
(乙)峰谷电价:峰时(早8:00~晚21:00)0.56元/度;谷时(晚21:00~早8:00)0.36元/度.
估计小明家下月总用电量为200度,
⑴若其中峰时电量为50度,则小明家按照哪种方式付电费比较合适?能省多少元?
⑵请你帮小明计算,峰时电量为多少度时,两种方式所付的电费相等?
⑶到下月付费时, 小明发现那月总用电量为200度,用峰谷电价付费方式比普通电价付费方式省了14元,求那月的峰时电量为多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中,F是AD的中点,延长BC到点E,使CE=
ABCD中,F是AD的中点,延长BC到点E,使CE=![]() BC,连结DE,CF。
BC,连结DE,CF。

(1)求证:四边形CEDF是平行四边形;
(2)若AB=4,AD=6,∠B=60°,求DE的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com