
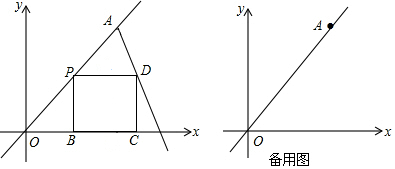
·ÖĪö £Ø1£©ÉčA£Øa£¬b£©£¬øł¾Żøł¾ŻČż½ĒŗÆŹżµÄ¶ØŅ壬ŅŌ¼°OAµÄ³¤ĮŠ³ö·½³Ģ£¬¼“æÉĒó³öaÓėbµÄÖµ£¬¼“æÉČ·¶Ø³öAµÄ×ų±ź£»
£Ø2£©øł¾ŻS”÷APD=$\frac{1}{2}$•AP•PDsin”ĻAPD¹¹½Ø¶ž“ĪŗÆŹż£¬¼“æÉĄūÓƶž“ĪŗÆŹżµÄŠŌÖŹ½ā¾öĪŹĢā£®
£Ø3£©¢ŁÓÉ”÷APD”×”÷AOE£¬ĶĘ³ö $\frac{PD}{OE}$=$\frac{AP}{AO}$£¬ĮŠ³ö·½³Ģ¼“æɽā¾öĪŹĢā£®
¢ŚÓÉDCÓėOCµÄ±Čֵȷ¶Ø£¬ČōČż½ĒŠĪOCDÓėČż½ĒŠĪDCEĻąĖĘ£¬µĆ±ČĄżĒó³ömµÄÖµ¼“æÉ£®
½ā“š ½ā£ŗ£Ø1£©ÉčA£Øa£¬b£©£¬×÷AF”ĶOEÓŚF£®
cos”ĻAOF=$\frac{a}{OA}$=$\frac{3}{5}$£¬¼“a=$\frac{3}{5}$”Į10=6£¬sin”ĻAOF=$\frac{b}{OA}$=$\frac{4}{5}$£¬¼“b=$\frac{4}{5}$”Į10=8£¬
ŌņA£Ø6£¬8£©£»
£Ø2£©”ßsin”ĻAOB=$\frac{4}{5}$£¬sin”ĻAPD=sin”ĻAOB=$\frac{4}{5}$£¬
”ßAP=OA-OP=10-m£¬$\frac{4}{5}$=$\frac{PB}{OP}$=$\frac{PB}{m}$£¬¼“PB=PD=$\frac{4}{5}$m£¬
”ąS”÷APD=$\frac{1}{2}$AP•PDsin”ĻAPD=$\frac{1}{2}$”Į$\frac{4}{5}$”Į£Ø10-m£©”Į$\frac{4}{5}$mØT-$\frac{8}{25}$m2+$\frac{80}{25}$m£¬
ŌņS”÷APDÓŠ×ī“óÖµ£¬µ±m=5Ź±£¬Smax=8£»
£Ø3£©¢Ł”ß”÷APD”×”÷AOE£¬
”ą$\frac{PD}{OE}$=$\frac{AP}{AO}$£¬¼“ $\frac{\frac{4}{5}m}{OE}$=$\frac{10-m}{10}$£¬
ÕūĄķµĆ£ŗOE=$\frac{8m}{10-m}$£¬
¢Ś”ßDCÓėOC³É¹Ģ¶Ø±ČĄż $\frac{4}{7}$£¬
Čō”÷OCD”×”÷DCE£¬ŌņÓŠ $\frac{CE}{DC}$=$\frac{DC}{OC}$=$\frac{4}{7}$£¬¼“ $\frac{\frac{8m}{10-m}-\frac{7}{5}m}{\frac{4}{5}m}$=$\frac{4}{7}$£¬
½āµĆ£ŗm=$\frac{74}{13}$£®
Čō”÷OCD”×”÷ECD£¬ŌņÓŠ$\frac{CD}{EC}$=$\frac{DC}{OC}$=$\frac{4}{7}$£¬
”ą$\frac{\frac{4}{5}m}{\frac{8m}{10-m}-\frac{7}{5}m}$=$\frac{4}{7}$£¬
½āµĆm=$\frac{50}{7}$£¬
×ŪÉĻĖłŹö£¬mµÄÖµĪŖ$\frac{74}{13}$»ņ$\frac{50}{7}$£®
µćĘĄ ±¾Ģāæ¼²éĻąĖĘČż½ĒŠĪ×ŪŗĻĢā”¢Čń½ĒČż½ĒŗÆŹż¶ØŅå”¢Čż½ĒŠĪĆ껿¹«Ź½£¬×ų±źÓėĶ¼ŠĪŠŌÖŹ£¬ĻąĖĘČż½ĒŠĪµÄÅŠ¶ØÓėŠŌÖŹ£¬½āĢāµÄ¹Ų¼üŹĒĮé»īŌĖÓĆĖłŃ§ÖŖŹ¶½ā¾öĪŹĢā£¬Ń§»įÓĆ·ÖĄąĢÖĀŪµÄĖ¼ĻėĖ¼æ¼ĪŹĢā£¬ŹōÓŚÖŠæ¼Ń¹ÖįĢā£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
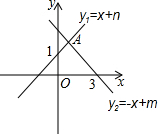 ČēĶ¼ĖłŹ¾£¬Ö±Ļßy1=x+nÓėyÖį½»ÓŚµć£Ø0£¬1£©£¬Ö±Ļßy2=-x+mÓėxÖį½»ÓŚµć£Ø3£¬0£©£¬Į½Ö±Ļß½»ÓŚµćA£®²»µČŹ½x+n”Ż-x+mµÄ½ā¼ÆĪŖx”Ż1£®
ČēĶ¼ĖłŹ¾£¬Ö±Ļßy1=x+nÓėyÖį½»ÓŚµć£Ø0£¬1£©£¬Ö±Ļßy2=-x+mÓėxÖį½»ÓŚµć£Ø3£¬0£©£¬Į½Ö±Ļß½»ÓŚµćA£®²»µČŹ½x+n”Ż-x+mµÄ½ā¼ÆĪŖx”Ż1£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
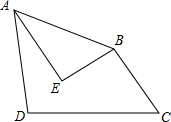
 ŅŃÖŖµČ±ß”÷ABCÖŠ£¬µćD£¬E·Ö±šŌŚ±ßAB£¬BCÉĻ£¬°Ń”÷BDEŃŲÖ±ĻßDE·ÕŪ£¬Ź¹µćBĀäŌŚµćB”䓦£¬DB”䣬EB”ä·Ö±š½»±ßACÓŚµćF£¬G£¬Čō”ĻADF=60”ć£¬Ōņ”ĻEGCµÄ¶ČŹżĪŖ60”ć£®
ŅŃÖŖµČ±ß”÷ABCÖŠ£¬µćD£¬E·Ö±šŌŚ±ßAB£¬BCÉĻ£¬°Ń”÷BDEŃŲÖ±ĻßDE·ÕŪ£¬Ź¹µćBĀäŌŚµćB”䓦£¬DB”䣬EB”ä·Ö±š½»±ßACÓŚµćF£¬G£¬Čō”ĻADF=60”ć£¬Ōņ”ĻEGCµÄ¶ČŹżĪŖ60”ć£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
 ČēĶ¼£¬ŌŚĖıߊĪABCDÖŠ£¬AB=AD£¬”ĻBAD=”ĻC=60”ć£¬µćEĪŖĖıߊĪABCDÄŚ²æŅ»µć£¬Į¬½ÓAE”¢BE£¬”ĻAEB=”ĻCBE=90”ć£¬BC=3£¬ŌņĻ߶ĪBEµÄ³¤ĪŖ$\frac{3\sqrt{3}}{2}$£®
ČēĶ¼£¬ŌŚĖıߊĪABCDÖŠ£¬AB=AD£¬”ĻBAD=”ĻC=60”ć£¬µćEĪŖĖıߊĪABCDÄŚ²æŅ»µć£¬Į¬½ÓAE”¢BE£¬”ĻAEB=”ĻCBE=90”ć£¬BC=3£¬ŌņĻ߶ĪBEµÄ³¤ĪŖ$\frac{3\sqrt{3}}{2}$£®²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com